3. Exploring an Algal Bloom with Band Math#
BioSCape, the Biodiversity Survey of the Cape, is NASA’s first biodiversity-focused airborne and field campaign that was conducted in South Africa in 2023. BioSCape’s primary objective is to study the structure, function, and composition of the region’s ecosystems, and how and why they are changing.
BioSCape’s airborne dataset is unprecedented, with AVIRIS-NG, PRISM, and HyTES imaging spectrometers capturing spectral data across the UV, visible and infrared at high resolution and LVIS acquiring coincident full-waveform lidar. BioSCape’s field dataset is equally impressive, with 18 PI-led projects collecting data ranging from the diversity and phylogeny of plants, kelp and phytoplankton, eDNA, landscape acoustics, plant traits, blue carbon accounting, and more
This workshop will equip participants with the skills to find, subset, and visualize the various BioSCape field and airborne (imaging spectroscopy and full-waveform lidar) data sets. Participants will learn data skills through worked examples in terrestrial and aquatic ecosystems, including: wrangling lidar data, performing band math calculations, calculating spectral diversity metrics, spectral unmixing, machine learning and image classification, and mapping functional traits using partial least squares regression. The workshop format is a mix of expert talks and interactive coding notebooks and will be run through the BioSCape Cloud computing environment.
Date: October 9 - 11, 2024 Cape Town, South Africa
Host: NASA’s Oak Ridge National Laboratory Distributed Active Archive Center (ORNL DAAC), in close collaboration with BioSCape, the South African Environmental Observation Network (SAEON), the University of Wisconsin Madison (Phil Townsend), The Nature Conservancy (Glenn Moncrieff), the University of California Merced (Erin Hestir), the University of Cape Town (Jasper Slingsby), Jet Propulsion Laboratory (Kerry Cawse-Nicholson), and UNESCO.
Instructors:
In-person contributors: Anabelle Cardoso, Erin Hestir, Phil Townsend, Henry Frye, Glenn Moncrieff, Jasper Slingsby, Michele Thornton, Rupesh Shrestha
Virtual contributors: Kerry Cawse-Nicholson, Nico Stork, Kyle Kovach
Audience: This training is primarily intended for government natural resource management agency representatives and field technicians in South Africa, as well as local academics and students, especially those connected to the BioSCape Team.
3.1. Exploring an algal bloom with PRISM data#
3.1.1. Overview#
In November 2023 the BioSCape campaign captured a red tide event - a bloom of noctiluca scintillans in Gordon’s Bay.

RGB image of the PRISM data acquired over Gordon’s Bay on November 15, 2023.
The event prompting local news outlets to report on residents’ complaints over smells, and reminding local residents to avoid swimming in the area.

Picture: Facebook/Anirie Taljaardt via Daily Voice
In this tutorial, we will practice opening PRISM data, and will learn how to apply simple band math statements and functions to an image to explore this algal bloom event in Gordon’s Bay.
3.1.2. Learning Objectives#
Gain proficiency in accessing PRISM data through the SMCE and S3 server and querying bands
Gain proficiency in plotting image spectra for a specified pixel
Apply band math statements to PRISM data to map fluorescence line height, chlorophyll-a concentration and absorption by colored dissolved organic matter
Gain proficiency in exporting derived maps as GeoTIFFs.
3.1.3. Requirements#
import s3fs
import matplotlib.pyplot as plt
from osgeo import gdal
import numpy as np
import pandas as pd
from os import path
import rioxarray
gdal.UseExceptions()
3.1.4. Content#
At this point, you should be increasingly familiar with accessing BioSCape data through the SMCE and S3 cloud storage service. As a reminder, SMCE = Science Managed Cloud Environment S3 = Amazon Simple Storage Service (S3) is a cloud storage service that allows users to store and retrieve data S3Fs is a Pythonic open source tool that mounts S3 object storage locally. S3Fs provides a filesystem-like interface for accessing objects on S3. The top-level class S3FileSystem holds connection information and allows typical file-system style operations like ls ls is a UNIX command to list computer files and directories
We are going to open a PRISM flightline acquired over Gordon’s Bay on November 15, 2023.
Recall that we are accessing PRISM reflectance Data as a GDAL Raster Dataset. GDAL (Geospatial Data Abstraction Library) is a translator library for raster and vector geospatial data formats In this step, we will use GDAL to examine the PRISM reflectance data that is in ENVI binary format (a proprietary, but common distribution format)
We need to configure our S3 credentials for GDAL The GDAL utility expects S3 links to be formated with the GDAL virtual file system (VSI) S3 path. We therefore have to use the VSI path to access the files with GDAL. We’ll substitute the S3 link with the VSI (vsis3) link(s).
# Gordon's Bay scene
rfl_link = 'bioscape-data/PRISM/L2/prm20231115t092332_rfl_ort'
image_open = gdal.Open(path.join('/vsis3', rfl_link))
#image_open.GetMetadata()
Take note of the bands numbers and corresponding wavelengths we are printing. We are going to need this information for our analysis.
# lists of band numbers and band center
band_numbers = [int(b.split("_")[1]) for b in image_open.GetMetadata().keys() if b != "wavelength_units"]
band_wavelength = [float(b.split(" ")[0]) for b in image_open.GetMetadata().values() if b != "Nanometers"]
# data frame describing bands
bands = pd.DataFrame({
"Band number": band_numbers,
"Band wavelength (nm)": band_wavelength}, index = band_wavelength).sort_index()
print(bands.to_string())
Band number Band wavelength (nm)
350.554829 1 350.554829
353.385086 2 353.385086
356.215399 3 356.215399
359.045768 4 359.045768
361.876193 5 361.876193
364.706675 6 364.706675
367.537213 7 367.537213
370.367807 8 370.367807
373.198457 9 373.198457
376.029164 10 376.029164
378.859927 11 378.859927
381.690746 12 381.690746
384.521621 13 384.521621
387.352553 14 387.352553
390.183541 15 390.183541
393.014585 16 393.014585
395.845685 17 395.845685
398.676841 18 398.676841
401.508054 19 401.508054
404.339323 20 404.339323
407.170649 21 407.170649
410.002030 22 410.002030
412.833468 23 412.833468
415.664962 24 415.664962
418.496512 25 418.496512
421.328118 26 421.328118
424.159781 27 424.159781
426.991500 28 426.991500
429.823275 29 429.823275
432.655106 30 432.655106
435.486994 31 435.486994
438.318938 32 438.318938
441.150938 33 441.150938
443.982994 34 443.982994
446.815107 35 446.815107
449.647276 36 449.647276
452.479501 37 452.479501
455.311782 38 455.311782
458.144120 39 458.144120
460.976514 40 460.976514
463.808964 41 463.808964
466.641470 42 466.641470
469.474033 43 469.474033
472.306651 44 472.306651
475.139326 45 475.139326
477.972058 46 477.972058
480.804845 47 480.804845
483.637689 48 483.637689
486.470589 49 486.470589
489.303545 50 489.303545
492.136557 51 492.136557
494.969626 52 494.969626
497.802751 53 497.802751
500.635932 54 500.635932
503.469169 55 503.469169
506.302463 56 506.302463
509.135813 57 509.135813
511.969219 58 511.969219
514.802681 59 514.802681
517.636200 60 517.636200
520.469775 61 520.469775
523.303406 62 523.303406
526.137093 63 526.137093
528.970837 64 528.970837
531.804637 65 531.804637
534.638493 66 534.638493
537.472405 67 537.472405
540.306373 68 540.306373
543.140398 69 543.140398
545.974479 70 545.974479
548.808616 71 548.808616
551.642810 72 551.642810
554.477060 73 554.477060
557.311366 74 557.311366
560.145728 75 560.145728
562.980146 76 562.980146
565.814621 77 565.814621
568.649152 78 568.649152
571.483739 79 571.483739
574.318382 80 574.318382
577.153082 81 577.153082
579.987838 82 579.987838
582.822650 83 582.822650
585.657518 84 585.657518
588.492443 85 588.492443
591.327424 86 591.327424
594.162461 87 594.162461
596.997554 88 596.997554
599.832704 89 599.832704
602.667910 90 602.667910
605.503172 91 605.503172
608.338490 92 608.338490
611.173865 93 611.173865
614.009295 94 614.009295
616.844782 95 616.844782
619.680325 96 619.680325
622.515925 97 622.515925
625.351581 98 625.351581
628.187293 99 628.187293
631.023061 100 631.023061
633.858885 101 633.858885
636.694766 102 636.694766
639.530703 103 639.530703
642.366696 104 642.366696
645.202745 105 645.202745
648.038851 106 648.038851
650.875013 107 650.875013
653.711231 108 653.711231
656.547505 109 656.547505
659.383836 110 659.383836
662.220223 111 662.220223
665.056666 112 665.056666
667.893165 113 667.893165
670.729721 114 670.729721
673.566333 115 673.566333
676.403001 116 676.403001
679.239725 117 679.239725
682.076505 118 682.076505
684.913342 119 684.913342
687.750235 120 687.750235
690.587185 121 690.587185
693.424190 122 693.424190
696.261252 123 696.261252
699.098370 124 699.098370
701.935544 125 701.935544
704.772774 126 704.772774
707.610061 127 707.610061
710.447404 128 710.447404
713.284803 129 713.284803
716.122258 130 716.122258
718.959770 131 718.959770
721.797338 132 721.797338
724.634962 133 724.634962
727.472642 134 727.472642
730.310379 135 730.310379
733.148172 136 733.148172
735.986021 137 735.986021
738.823926 138 738.823926
741.661888 139 741.661888
744.499906 140 744.499906
747.337980 141 747.337980
750.176110 142 750.176110
753.014297 143 753.014297
755.852539 144 755.852539
758.690838 145 758.690838
761.529194 146 761.529194
764.367605 147 764.367605
767.206073 148 767.206073
770.044597 149 770.044597
772.883177 150 772.883177
775.721813 151 775.721813
778.560506 152 778.560506
781.399255 153 781.399255
784.238060 154 784.238060
787.076921 155 787.076921
789.915839 156 789.915839
792.754813 157 792.754813
795.593843 158 795.593843
798.432929 159 798.432929
801.272072 160 801.272072
804.111271 161 804.111271
806.950526 162 806.950526
809.789837 163 809.789837
812.629205 164 812.629205
815.468629 165 815.468629
818.308109 166 818.308109
821.147645 167 821.147645
823.987237 168 823.987237
826.826886 169 826.826886
829.666591 170 829.666591
832.506353 171 832.506353
835.346170 172 835.346170
838.186044 173 838.186044
841.025974 174 841.025974
843.865960 175 843.865960
846.706002 176 846.706002
849.546101 177 849.546101
852.386256 178 852.386256
855.226467 179 855.226467
858.066734 180 858.066734
860.907058 181 860.907058
863.747438 182 863.747438
866.587874 183 866.587874
869.428366 184 869.428366
872.268915 185 872.268915
875.109520 186 875.109520
877.950181 187 877.950181
880.790898 188 880.790898
883.631672 189 883.631672
886.472502 190 886.472502
889.313388 191 889.313388
892.154330 192 892.154330
894.995328 193 894.995328
897.836383 194 897.836383
900.677494 195 900.677494
903.518662 196 903.518662
906.359885 197 906.359885
909.201165 198 909.201165
912.042501 199 912.042501
914.883893 200 914.883893
917.725341 201 917.725341
920.566846 202 920.566846
923.408407 203 923.408407
926.250024 204 926.250024
929.091697 205 929.091697
931.933427 206 931.933427
934.775213 207 934.775213
937.617055 208 937.617055
940.458953 209 940.458953
943.300908 210 943.300908
946.142919 211 946.142919
948.984986 212 948.984986
951.827109 213 951.827109
954.669289 214 954.669289
957.511525 215 957.511525
960.353817 216 960.353817
963.196165 217 963.196165
966.038569 218 966.038569
968.881030 219 968.881030
971.723547 220 971.723547
974.566121 221 974.566121
977.408750 222 977.408750
980.251436 223 980.251436
983.094178 224 983.094178
985.936976 225 985.936976
988.779830 226 988.779830
991.622741 227 991.622741
994.465708 228 994.465708
997.308731 229 997.308731
1000.151810 230 1000.151810
1002.994946 231 1002.994946
1005.838138 232 1005.838138
1008.681386 233 1008.681386
1011.524690 234 1011.524690
1014.368051 235 1014.368051
1017.211468 236 1017.211468
1020.054941 237 1020.054941
1022.898470 238 1022.898470
1025.742056 239 1025.742056
1028.585698 240 1028.585698
1031.429396 241 1031.429396
1034.273150 242 1034.273150
1037.116961 243 1037.116961
1039.960827 244 1039.960827
1042.804750 245 1042.804750
1045.648730 246 1045.648730
# need to sort the wavelengths for later plotting
band_wavelength.sort()
#print(band_wavelength)
# Open the PRISM ENVI file and read the file bands, row, cols
#image_open = gdal.Open(gdal_url)
nbands = image_open.RasterCount
nrows = image_open.RasterYSize
ncols = image_open.RasterXSize
print("\n".join(["Bands:\t"+str(nbands), "Rows:\t"+str(nrows), "Cols:\t"+str(ncols)]))
Bands: 246
Rows: 5459
Cols: 697
3.1.4.1. Compare Spectra from Two Pixels in the Bloom#
# Compare spectra of two different aquatic plots
pixel1 = image_open.ReadAsArray(393, 2487, 1, 1) # pixel location: col, row
pixel2 = image_open.ReadAsArray(475, 2490, 1, 1) # pixel location: col, row
pixel1 = np.reshape(pixel1, (246))
pixel2 = np.reshape(pixel2, (246))
plt.rcParams['figure.figsize'] = [15,7]
plt.plot(band_wavelength, pixel1, color = 'red')
plt.plot(band_wavelength, pixel2, color = 'black')
plt.xlabel('PRISM Wavelength (nm)', fontsize=12)
plt.ylabel('Reflectance', fontsize=12)
plt.show()
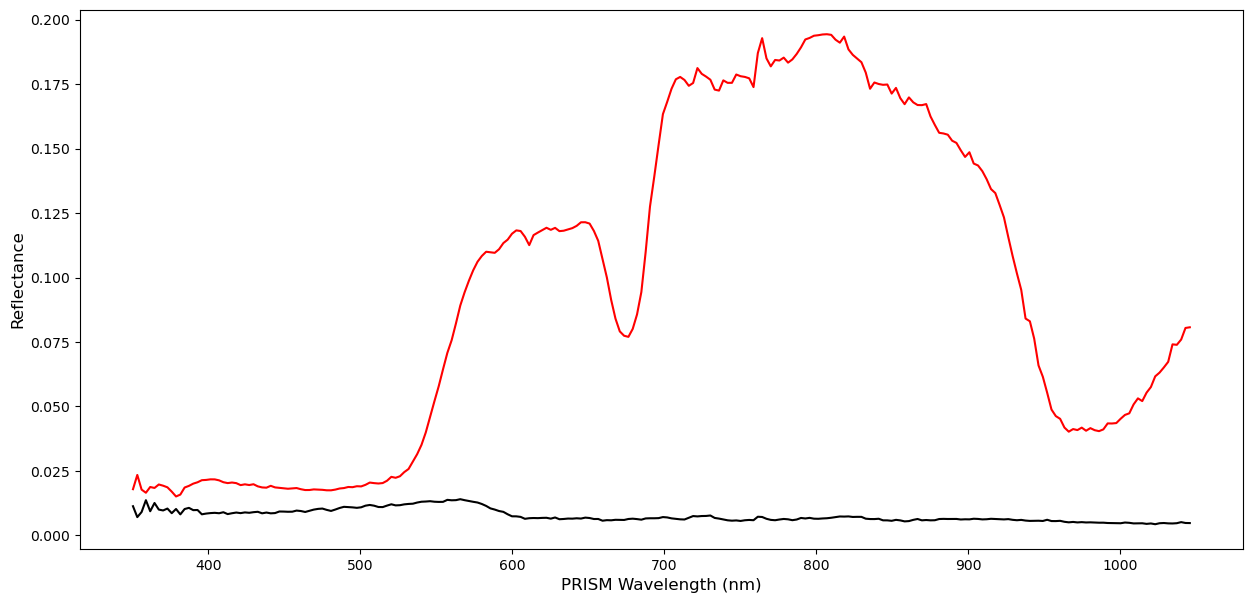
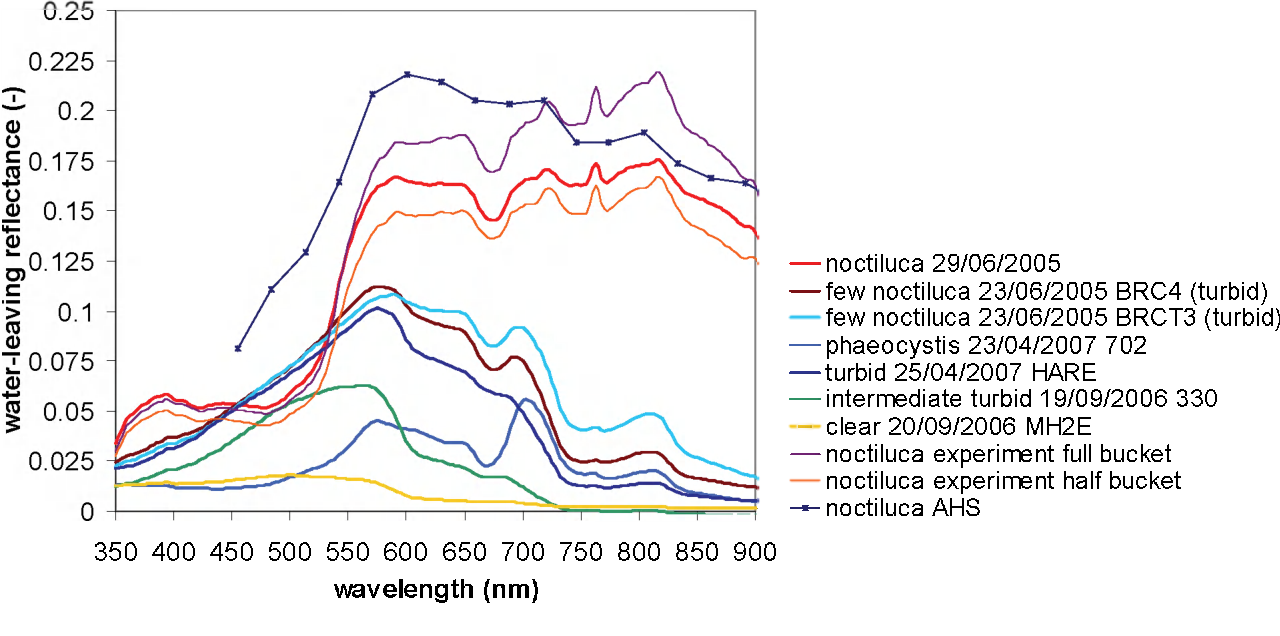
This looks similar to field spectrscopy collected by Mol et al. (2007) of a noctiluca bloom.
This is a good sanity check!
3.1.5. Calculate Fluorescence Line height (FLH)#
The [Fluorescence Line Height] (FLH)(https://www.sciencedirect.com/science/article/pii/S0034425796000739) is typically calculated by estimating the height of the chlorophyll fluorescence peak at around 681 nm using two other bands on either side of this peak to form a baseline.
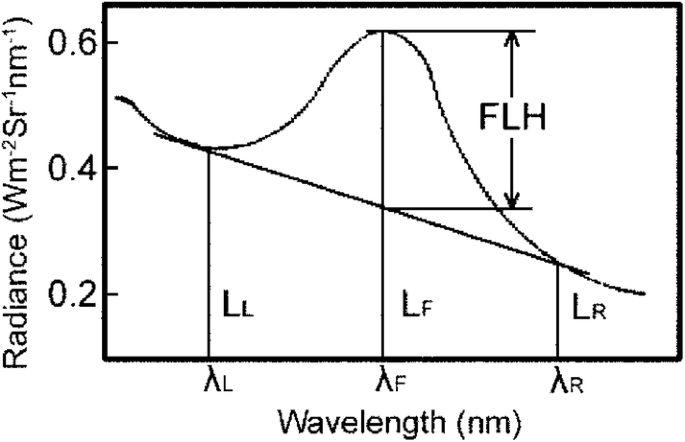
Concept of the FLH measurement, taken from Umamaheswara Rao et al. (2019).
The chlorophyll fluoresence peak occurs around 681 nm. We select two bands on either side, typically around 665 nm (the lower wavelength band) and 750 nm (the higher wavelength band).
The general formula for FLH is:
Where
\(L_{fl}\) is the water-leaving radiance at the fluorescence peak (~681 nm)
\(L_{low}\) and \(L_{high}\) are the radiance values at the shorter and longer wavelengths adjacent to the fluorescence band.
\(\lambda_{fl}\), \(\lambda_{low}\), and \(\lambda_{high}\) are the wavelengths corresponding to those bands.
3.1.5.1. A Note on Water Leaving Radiance vs Remote Sensing Reflectance#
Fluorescence Line Height (FLH) is typically calculated using water-leaving radiance (\(L_{w}\)), not remote sensing reflectance (\(R_{RS}\)). The key difference is:
Water-leaving radiance (\(L_{w}\))is the radiance that exits the water and is detected by a satellite sensor after traveling through the atmosphere.
Remote sensing reflectance (\(R_{RS}\))is the ratio of water-leaving radiance to downwelling irradiance just above the surface of the water, representing a normalized reflectance value.
Why Use Water-leaving Radiance for FLH? FLH measures the fluorescence signal of chlorophyll-a at around 681 nm. The calculation of FLH is done directly from the radiance values because the fluorescence signal itself is an addition to the radiance at that wavelength, caused by chlorophyll fluorescence in the water column. It captures the deviation in radiance at the chlorophyll fluorescence wavelength (around 681 nm) compared to the baseline radiance, which is estimated by interpolating between radiance at surrounding bands.
How do we convert between \(R_{RS}\) and \(L_w\)? $\( L_w = \pi R_{RS}\)$
We are going to read in three bands
img_665 = image_open.GetRasterBand(112).ReadAsArray() # Band 112 is 665nm
img_682 = image_open.GetRasterBand(118).ReadAsArray() # Band 181 is 682nm
img_750 = image_open.GetRasterBand(142).ReadAsArray() # Band 142 is 750nm
# Wavelength values (in nm)
lambda_low = 665
lambda_fl = 680
lambda_high = 750
# Convert RRS to Lw
img_682_Lw = img_682*np.pi
img_665_Lw = img_665*np.pi
img_750_Lw = img_750*np.pi
# Calculate FLH using the formula
FLH = img_682_Lw - (img_665_Lw + ((lambda_fl - lambda_low) / (lambda_high - lambda_low)) * (img_750_Lw - img_665_Lw))
# Compare FLH values of two different pixels
# Note here when we print an element in a numpy array, the order is row column
pixel1 = FLH[2487, 393] # pixel location: row, col
pixel2 = FLH[2490, 475] # pixel location: row, col
print("The FLH value at pixel 1 is " + str(pixel1))
print("The FLH value at pixel 2 is " + str(pixel2))
The FLH value at pixel 1 is -0.06581387
The FLH value at pixel 2 is 0.0016050916
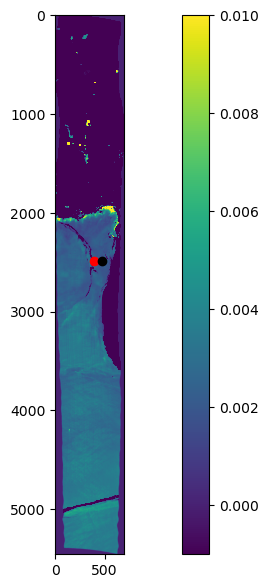
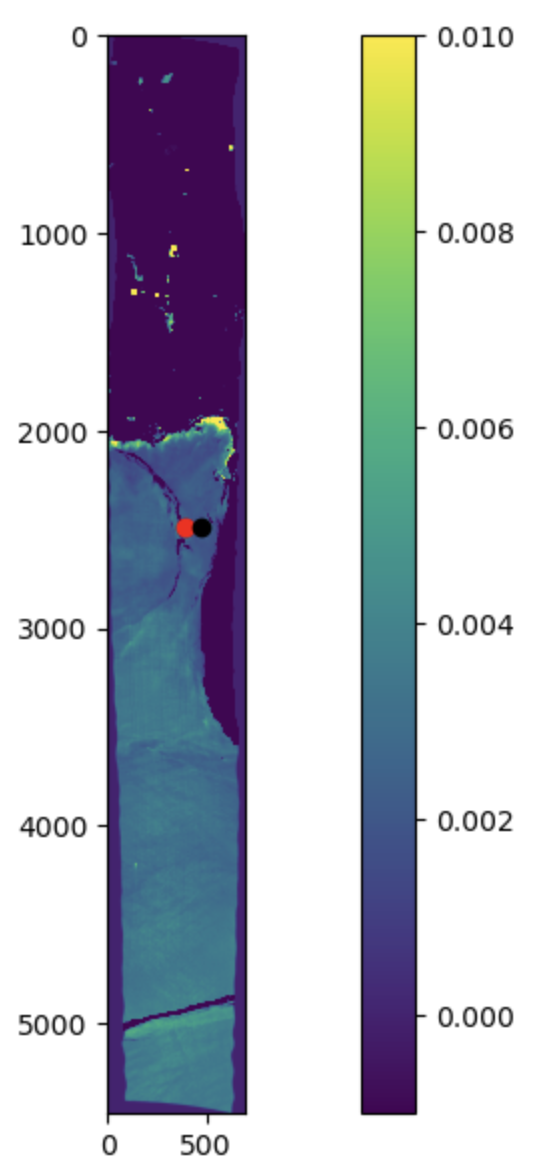
plt.scatter(393,2487, color='red')
plt.scatter(475, 2490, color='black')
plt.rcParams['figure.figsize'] = [10,10]
plt.rcParams['figure.dpi'] = 100
plt.imshow(FLH, vmin=-0.001, vmax=0.01)
plt.colorbar()
plt.show()
3.1.6. Calculate chlorophyll#
The OC2 algorithm is another empirical ocean color algorithm used to estimate chlorophyll-a concentration in ocean waters using a simple ratio of reflectance values from two spectral bands. OC2 typically uses two wavelengths, such as 490 nm (blue) and 555 nm (green). It is one of the oldest algorithms for chlorophyll-a, originally developed for the SeaWIFS ocean color instrument.
The OC2 algorithm was designed for ocean color satellite sensors like SeaWiFS, MODIS, or Sentinel-3. It takes the ratio of blue to green reflectance and empirically relates that ratio to chlorophyll concentration.
Where:
\(R_{490}\) is the reflectance at 490 nm
\(R_{555}\) is the reflectance at 550 nm
\(a_0, a_1, a_2, a_3\) are empirically derrived coefficients for a specific sensor and region
In this case, we will use the coefficients for Sentinel-3 OLCI
\(a_0 = 0.238\)
\(a_1 = -1.936\)
\(a_2 = 1.762\)
\(a_3 = -0.463\)
The OC2 algorithm is a good choice for estimating chlorophyll concentration in open ocean and coastal areas where the water is relatively clear. For more complex environments, a different algorithm or recalibration might be necessary. For more on the ocean color chlorophyll algorithms, see this recent overview.
We are going to read in two bands
img_489 = image_open.GetRasterBand(50).ReadAsArray() # Band 50 is 489nm
img_560 = image_open.GetRasterBand(75).ReadAsArray() # Band 75 is 560nm
# Calculate the ratio R between 490 nm and 560 nm reflectance
# Note that because we are calculating a ratio, conversion to/from Lw is not needed
R = img_489/img_560
# OC2 Coefficients for Sentinel-3 OLCI
a0, a1, a2, a3 = 0.238, -1.936, 1.762, -0.463
# Calculate log10(R)
log_R = np.log10(R)
# Estimate chlorophyll concentration (in mg/m^3) using the polynomial equation
log_C = a0 + a1 * log_R + a2 * log_R**2 + a3 * log_R**3
C = 10 ** log_C
# Compare Chl-a values of two different pixels
# Note here when we print an element in a numpy array, the order is row column
pixel1 = log_C[2487, 393] # pixel location: row, col
pixel2 = log_C[2490, 475] # pixel location: row, col
print("The log_C value at pixel 1 is " + str(pixel1))
print("The log_C value at pixel 2 is " + str(pixel2))
The log_C value at pixel 1 is 2.2050688
The log_C value at pixel 2 is 0.42584196
3.1.7. Calculate Colored Dissolved Organic Matter#
Calculating colored dissolved organic matter using spectrally adjacent band ratios has been demonstrated to be very successful across a broad range of oceanic and coastal waters. Most CDOM algorithms take the general form of a ratio of blue and green bands, blue and red, or green and red. The ratio is then used in a power-law model or exponential decay model to calibrate to absorption by CDOM, with coefficients that are empirically derived from field data.
In this example, we will use Housekeeper et al. 2021 model.
Where
\(R_{412}\) is the reflectance at 412 nm
\(R_{670}\) is the reflectance at 670 nm
\(a = 0.010\) and \(b = 0.036\)
We are going to read in two bands
img_412 = image_open.GetRasterBand(23).ReadAsArray() # Band 23 is 412nm
img_670 = image_open.GetRasterBand(114).ReadAsArray() # Band 114 is 670nm
3.1.7.1. Define a Function for Band Math#
If you haven’t noticed yet, we are essentially doing a lot of band math. Sometimes it can be more efficient and more elegant to define a function so we can apply it over and over again. We often want to use functions because they can:
increase the reusibility of code
save you a lot of time
make your code look cleaner, and thus easier to troubleshoot and share with others
In the example below, I will define a function for our algorithm so you can see an example.
# Function to calculate CDOM using a power law function of band ratios
def calculate_cdom_power_law(blue_band, green_band, a=1.0, b=1.5):
"""
Calculates CDOM using a power law function of band ratios.
Parameters:
blue_band: np.array - Reflectance values from the blue band (e.g., 490 nm)
green_band: np.array - Reflectance values from the green band (e.g., 560 nm)
a: float - Coefficient scaling factor (default=1.0)
b: float - Exponent for the power law (default=1.5)
Returns:
np.array: CDOM values
"""
# Avoid division by zero and invalid values
ratio = np.divide(blue_band, green_band, out=np.zeros_like(blue_band), where=green_band != 0)
# Apply the power law equation
cdom = a * np.power(ratio, b)
return cdom
# Parameters for the power law algorithm (adjust based on calibration)
a = 0.01 # From Housekeeper et al. 2021
b = 0.036 # From Housekeeper et al. 2021
# Calculate CDOM
cdom = calculate_cdom_power_law(img_412, img_670, a, b)
# Compare CDOM values of two different pixels
# Note here when we print an element in a numpy array, the order is row column
pixel1 = cdom[2487, 393] # pixel location: row, col
pixel2 = cdom[2490, 475] # pixel location: row, col
print("The CDOM value at pixel 1 is " + str(pixel1))
print("The CDOM value at pixel 2 is " + str(pixel2))
The CDOM value at pixel 1 is 0.009521637
The CDOM value at pixel 2 is 0.010113926
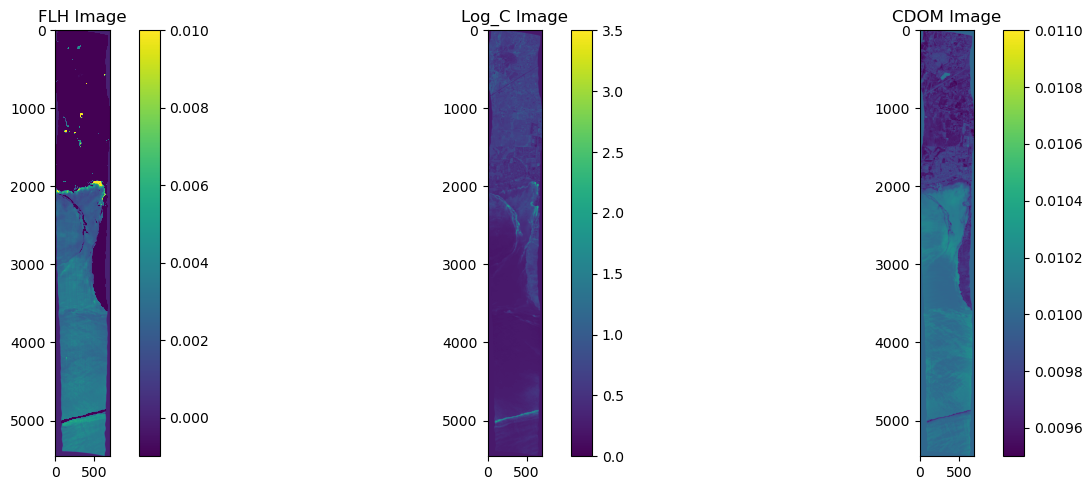
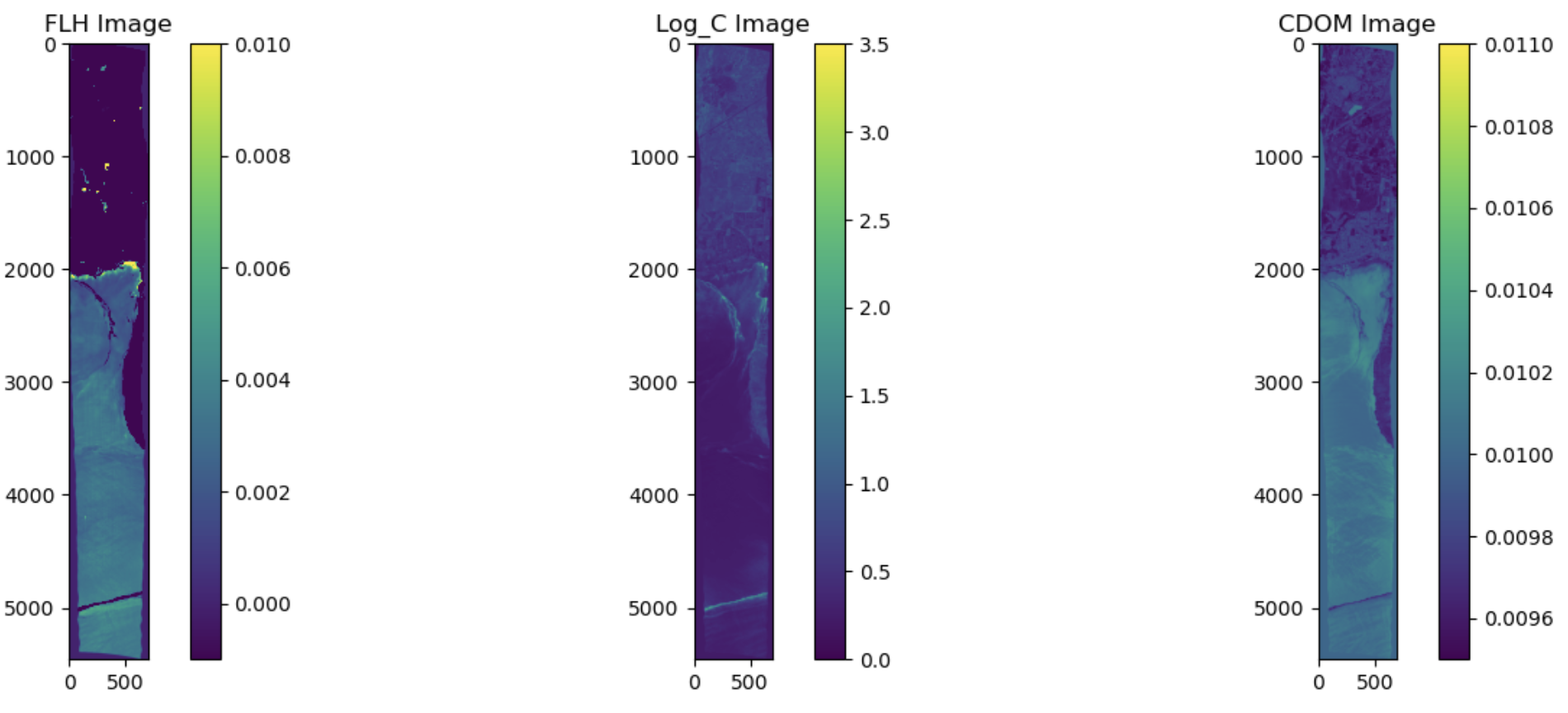
### Visualize all three maps side-by-side
import matplotlib.pyplot as plt
# Create a 1x3 grid of subplots
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
# First subplot (FLH image with scatter points)
img1 = axes[0].imshow(FLH, vmin=-0.001, vmax=0.01)
fig.colorbar(img1, ax=axes[0])
axes[0].set_title('FLH Image')
# Second subplot (log_C image with scatter points)
img2 = axes[1].imshow(log_C, vmin=0, vmax=3.5)
fig.colorbar(img2, ax=axes[1])
axes[1].set_title('Log_C Image')
# Third subplot (cdom image with scatter points)
img3 = axes[2].imshow(cdom, vmin=0.0095, vmax=0.011)
fig.colorbar(img3, ax=axes[2])
axes[2].set_title('CDOM Image')
# Adjust layout for better spacing
plt.tight_layout()
plt.show()
3.1.8. Export turbidity maps as a stacked projected geoTIFFs#
img_red = image_open.GetRasterBand(105).ReadAsArray() # Band 105 is 645nm red
outfile = ('prism_bloom.tif')
rows = image_open.RasterYSize
cols = image_open.RasterXSize
datatype = image_open.GetRasterBand(1).DataType
projection = image_open.GetProjection()
transform = image_open.GetGeoTransform()
driver = gdal.GetDriverByName("GTiff")
DataSetOut = driver.Create(outfile, cols, rows, 2, datatype) # 3 band stack
DataSetOut.GetRasterBand(1).WriteArray(FLH) # note the order of the band stack
DataSetOut.GetRasterBand(2).WriteArray(log_C)
DataSetOut.GetRasterBand(2).WriteArray(cdom)
DataSetOut.SetProjection(projection)
DataSetOut.SetGeoTransform(transform)
DataSetOut = None

