Exploring GEDI L4A data structure

This tutorial will explore data structure, variables, and quality flags of the Global Ecosystem Dynamics Investigation (GEDI) L4A Footprint Level Aboveground Biomass Density (AGBD)[Dubayah et al., 2022] dataset. GEDI L4A dataset is currently available for the period starting 2019-04-17 and covers 52 North to 52 South latitudes.

Details about the GEDI L4A dataset are available in the User Guide and the Algorithm Theoretical Basis Document (ATBD)] [Kellner et al., 2022]. Please refer to other tutorials for searching and downloading the GEDI L4A dataset and subsetting GEDI L4A footprints by area of interest.

Learning Objectives

• Understand GEDI L4A data structure, variables and quality flags (study area).

Requirements

Additional prerequisites are provided here.

# import all the modules
from os import path
from datetime import datetime
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import geopandas as gpd
import h5py
import earthaccess
from shapely.geometry import Point
from matplotlib_scalebar.scalebar import ScaleBar
from matplotlib.lines import Line2D
from matplotlib import colormaps
from matplotlib.colors import ListedColormap
from scipy import stats
import contextily as ctx
plt.style.use('seaborn-v0_8-whitegrid')

2. Example file

In this tutorial, we will use one GEDI L4A file, GEDI04_A_2020207182449_O09168_03_T03028_02_002_02_V002.h5. Let’s first search the file using the earthaccess module. Please refer to the previous tutorial for more details on downloading programmatically.

# GEDI L4a file
GEDIL4A = 'GEDI04_A_2020207182449_O09168_03_T03028_02_002_02_V002.h5'

# authenticate using the EDL login
try:
    auth = earthaccess.login(strategy="netrc")
except FileNotFoundError:
    auth = earthaccess.login(strategy="interactive", persist=True)

# search the granule
granules = earthaccess.search_data(
    doi="10.3334/ORNLDAAC/2056", # GEDI L4A DOI
    granule_name = f"*{GEDIL4A}",
)
# print the granule details
granules[0]

Data: GEDI04_A_2020207182449_O09168_03_T03028_02_002_02_V002.h5

Size: 358.96 MB

Cloud Hosted: True

The file is ~359 MB in size. We will go ahead and use earthaccess python module to get the file directly and save it to the full_orbits directory.

# download files to full_orbits directory
downloaded_files = earthaccess.download(granules, local_path="full_orbits")

GEDI footprints data, including the Level 4A, are natively in HDF5 format, and each file represents one of the four International Space Station (ISS). The file naming convention of the GEDI L4A is as GEDI04_A_YYYYDDDHHMMSS_O[orbit_number]_[granule_number]_T[track_number]_[PPDS_type]_ [release_number]_[production_version]_V[version_number].h5:

• GEDI04_A: product short name

• YYYYDDDHHMMSS: date and time of acquisition in Julian day of year, hours, minutes, and seconds format

• [orbit_number]: orbit number

• [granule_number]: sub-orbit granule (or file) number

• [track_number]: track number

• [PPDS_type]: positioning and pointing determination system (PPDS) type (00: predict, 01: rapid, > 02: final)

• [release_number]: release number 002, representing the SOC SDS (software) release

• [production_version]: granule production version

• [version_number]: dataset version

The GEDI L4A file GEDI04_A_2020207182449_O09168_03_T03028_02_002_02_V002.h5 represents orbit number 09168, sub-orbit 03, and track number 03028 for the starting date-time in YYYYDDDHHMMSS format 2020207182449 or 2020-07-25 18:24:49 UTC. The file has the PPDS type of 02, which means it is final quality data. The file has a granule production version of 02 and Version 002 (Release 002).

3. Root Groups

Let’s open this file using the h5py python library and print the root-level groups of the file.

l4af = path.join('full_orbits', GEDIL4A)
# read the L4A file
hf = h5py.File(l4af, 'r')
# printing root-level groups
list(hf.keys())

['ANCILLARY',
 'BEAM0000',
 'BEAM0001',
 'BEAM0010',
 'BEAM0011',
 'BEAM0101',
 'BEAM0110',
 'BEAM1000',
 'BEAM1011',
 'METADATA']

All science variables are organized by eight beams of the GEDI. Please refer to the GEDI L4A user guide and GEDI L4A data dictionary for details. The root-level group also includes ANCILLARY and METADATA groups.

3. METADATA group

The METADATA group contains information about the file metadata. All the metadata attributes are provided in the DatasetIdentification group within METADATA. Let’s print its content.

# read the METADATA group
metadata = hf['METADATA/DatasetIdentification']
# store attributes and descriptions in an array
data = []
for attr, desc in metadata.attrs.items():
    data.append([attr, desc])

# display `data` as a pandas table
df = pd.DataFrame(data, columns=['attribute', 'description'])
tbl_n = 1 # table number
caption = f'Table {tbl_n}. Attributes and discription from `METADATA` group'
df.style.set_caption(caption).hide(axis="index")

Table 1. Attributes and discription from `METADATA` group

attribute	description
PGEVersion	002
VersionID	02
abstract	The GEDI L4A standard data product contains predictions of aboveground biomass density within each laser footprint.
characterSet	utf8
creationDate	2022-02-21T10:02:04.611768Z
credit	The software that generates the L4A product was implemented at the Department of Geographical Sciences at the University of Maryland (UMD), in collaboration with the GEDI Science Data Processing System at the NASA Goddard Space Flight Center (GSFC) in Greenbelt, Maryland and the Institute at Brown for Environment and Society at Brown University.
fileName	GEDI04_A_2020207182449_O09168_03_T03028_02_002_02_V002.h5
gedi_l4a_githash	15f188fa6d18cd509186d8d36bea668faa22b1f5
language	eng
originatorOrganizationName	GSFC GEDI-SDPS > GEDI Science Data Processing System and University of Maryland
purpose	The purpose of the L4A dataset is to provide an estimate of aboveground biomass density from each GEDI waveform.
shortName	GEDI_L4A
spatialRepresentationType	along-track
status	onGoing
topicCategory	geoscientificInformation
uuid	97b127da-9915-4e71-8929-fdae799447b0

4. ANCILLARY group

The ANCILLARY group has three sub-groups - model_data, pft_lut, and region_lut.

# read the ANCILLARY group
ancillary = hf['ANCILLARY']
# print the subgroups
list(ancillary.keys())

['model_data', 'pft_lut', 'region_lut']

The model_data subgroup contains information about parameters and variables from the L4A models used to generate predictions. The details about model_data variables are available in ‘Table 6’ of the user guide. Let’s print the model_data variables.

# read model_data subgroup
model_data = ancillary['model_data']
# print variables, data types, data dimension
model_data.dtype

dtype([('predict_stratum', 'O'), ('model_group', 'u1'), ('model_name', 'O'), ('model_id', 'u1'), ('x_transform', 'O'), ('y_transform', 'O'), ('bias_correction_name', 'O'), ('fit_stratum', 'O'), ('rh_index', 'u1', (8,)), ('predictor_id', 'u1', (8,)), ('predictor_max_value', '<f4', (8,)), ('vcov', '<f8', (5, 5)), ('par', '<f8', (5,)), ('rse', '<f4'), ('dof', '<u4'), ('response_max_value', '<f4'), ('bias_correction_value', '<f4'), ('npar', 'u1')])

Some model_data parameters have more than one dimension (e.g., vcov, which is the variance-covariance matrix of model parameters, has a dimension of 5 x 5). First, let’s read all one-dimensional variables into a pandas dataframe.

# initialize an empty dataframe
model_data_df = pd.DataFrame()
# loop through parameters
for v in model_data.dtype.names:
    # exclude multidimensional variables
    if len(model_data[v].shape) == 1:
        # copy parameters as dataframe column
        model_data_df[v] = model_data[v]
        # converting object datatype to string
        if model_data_df[v].dtype.kind=='O':
            model_data_df[v] = model_data_df[v].str.decode('utf-8')

# print the parameters
tbl_n += 1
caption = f'Table {tbl_n}. Parameters and their values in `model_data` subgroup'
model_data_df.style.set_caption(caption).hide(axis="index")

Table 2. Parameters and their values in `model_data` subgroup

predict_stratum	model_group	model_name	model_id	x_transform	y_transform	bias_correction_name	fit_stratum	rse	dof	response_max_value	bias_correction_value	npar
DBT_Af	4	DBT_Af	3	sqrt	sqrt	Snowdon	DBT_Af	1.950498	487	386.758881	1.092463	3
DBT_Au	4	EBT_Au	1	sqrt	sqrt	Snowdon	EBT_Au	2.923645	210	830.582031	1.017920	3
DBT_Eu	4	DBT_Eu	1	sqrt	sqrt	Snowdon	Eu	2.818270	747	724.057983	0.962632	3
DBT_NAs	4	DBT_coarse	1	sqrt	sqrt	Snowdon	DBT	2.661183	1695	724.057983	1.016632	3
DBT_SA	4	EBT_SA	1	sqrt	sqrt	Snowdon	EBT_SA	3.439619	3438	1578.000000	1.105528	3
DBT_SAs	4	EBT_coarse	1	sqrt	sqrt	Snowdon	EBT	3.920913	4811	1578.000000	1.113366	3
DBT_NAm	4	DBT_NAm	1	sqrt	sqrt	Snowdon	NAm	3.126976	2279	1768.699341	1.052422	3
EBT_Af	4	EBT_Af	1	sqrt	sqrt	Snowdon	EBT	3.920913	4811	1578.000000	1.113366	3
EBT_Au	4	EBT_Au	1	sqrt	sqrt	Snowdon	EBT_Au	2.923645	210	830.582031	1.017920	3
EBT_Eu	4	DBT_Eu	1	sqrt	sqrt	Snowdon	Eu	2.818270	747	724.057983	0.962632	3
EBT_NAs	4	DBT_coarse	1	sqrt	sqrt	Snowdon	DBT	2.661183	1695	724.057983	1.016632	3
EBT_SA	4	EBT_SA	1	sqrt	sqrt	Snowdon	EBT_SA	3.439619	3438	1578.000000	1.105528	3
EBT_SAs	4	EBT_coarse	1	sqrt	sqrt	Snowdon	EBT	3.920913	4811	1578.000000	1.113366	3
EBT_NAm	4	DBT_NAm	1	sqrt	sqrt	Snowdon	NAm	3.126976	2279	1768.699341	1.052422	3
ENT_Af	4	ENT_coarse	4	sqrt	sqrt	Snowdon	ENT	3.292492	1983	1768.699341	1.018368	3
ENT_Au	3	ENT_Au	1	sqrt	sqrt	Snowdon	ENT_Au	3.075415	139	571.716431	0.897592	3
ENT_Eu	4	ENT_Eu	1	sqrt	sqrt	Snowdon	Eu	2.818270	747	724.057983	0.962632	3
ENT_NAs	4	ENT_coarse	4	sqrt	sqrt	Snowdon	ENT	3.292492	1983	1768.699341	1.018368	3
ENT_SA	4	ENT_coarse	4	sqrt	sqrt	Snowdon	ENT	3.292492	1983	1768.699341	1.018368	3
ENT_SAs	4	ENT_coarse	4	sqrt	sqrt	Snowdon	ENT	3.292492	1983	1768.699341	1.018368	3
ENT_NAm	4	ENT_NAm	2	sqrt	sqrt	Snowdon	ENT	3.310075	1983	1768.699341	1.012534	3
DNT_Af	4	ENT_coarse	4	sqrt	sqrt	Snowdon	ENT	3.292492	1983	1768.699341	1.018368	3
DNT_Au	3	ENT_Au	1	sqrt	sqrt	Snowdon	ENT_Au	3.075415	139	571.716431	0.897592	3
DNT_Eu	4	ENT_Eu	1	sqrt	sqrt	Snowdon	Eu	2.818270	747	724.057983	0.962632	3
DNT_NAs	4	ENT_coarse	4	sqrt	sqrt	Snowdon	ENT	3.292492	1983	1768.699341	1.018368	3
DNT_SA	4	ENT_coarse	4	sqrt	sqrt	Snowdon	ENT	3.292492	1983	1768.699341	1.018368	3
DNT_SAs	4	ENT_coarse	4	sqrt	sqrt	Snowdon	ENT	3.292492	1983	1768.699341	1.018368	3
DNT_NAm	4	ENT_NAm	2	sqrt	sqrt	Snowdon	ENT	3.310075	1983	1768.699341	1.012534	3
GSW_Af	4	GSW_coarse	1	sqrt	sqrt	Snowdon	GSW	1.626275	87	192.562592	1.118195	2
GSW_Au	4	GSW_Au	3	sqrt	sqrt	Snowdon	GSW	1.637400	85	192.562592	1.127970	4
GSW_Eu	4	GSW_coarse	1	sqrt	sqrt	Snowdon	GSW	1.626275	87	192.562592	1.118195	2
GSW_NAs	4	GSW_coarse	1	sqrt	sqrt	Snowdon	GSW	1.626275	87	192.562592	1.118195	2
GSW_SA	4	GSW_coarse	1	sqrt	sqrt	Snowdon	GSW	1.626275	87	192.562592	1.118195	2
GSW_SAs	4	GSW_coarse	1	sqrt	sqrt	Snowdon	GSW	1.626275	87	192.562592	1.118195	2
GSW_NAm	4	GSW_coarse	1	sqrt	sqrt	Snowdon	GSW	1.626275	87	192.562592	1.118195	2

The predict_stratum names are divided into two parts - the first part corresponding to PFTs and the second part to world regions.

PFTs (corresponding MCD12Q1 V006 classes are in parenthesis)
DBT: deciduous broadleaf trees (Class 4), DNT: deciduous needleleaf trees (Class 3), EBT: evergreen broadleaf trees (Class 2), ENT: evergreen needleleaf trees (Class 1), GSW: grasses, shrubs and woodlands (Classes 5, 6, 11)

World Regions
Af: Africa, Au: Australia and Oceania, Eu: Europe, NAm : North America, NAs: North Asia, SA: South America, SAs : South Asia

The information on PFTs and World Regions are also provided in pft_lut and region_lut groups within the ANCILLARY group.

# read pft_lut subgroup
pft_lut = ancillary['pft_lut']
headers = pft_lut.dtype.names
# print pft class and names
df = pd.DataFrame(zip(pft_lut[headers[0]], pft_lut[headers[1]]),
                  columns=headers) 
df.pft_name = df.pft_name.apply(lambda x: x.decode('utf-8'))
df.style.hide(axis="index")

pft_class	pft_name
1	ENT
3	DNT
2	EBT
4	DBT
5	GSW
6	GSW
11	GSW

# read region_lut subgroup
region_lut = ancillary['region_lut']
headers = region_lut.dtype.names
# print region class and names
df = pd.DataFrame(zip(region_lut[headers[0]], region_lut[headers[1]]),
                  columns=headers) 
df.region_name = df.region_name.apply(lambda x: x.decode('utf-8'))
df.style.hide(axis="index")

region_class	region_name
1	Eu
2	NAs
5	SAs
3	Au
4	Af
6	SA
7	NAm

In Table 2 above, the model_group column represents model group:

Model Group
1: all predictors considered, 2: no RH metrics below RH50, 3: forced inclusion of RH98, 4: forced inclusion of RH98 and no RH metrics below RH50

x_transform and y_transform are predictor and response transform functions (e.g., sqrt, log). The column bias_correction_name specifies the bias correction methods used - Snowdon (1991) or Baskerville (1972). For details, please refer to Section 4.3 of the ATBD.

To retrieve values from multidimensional variables, we can directly slice using the index from pandas dataframe model_data_df. For example, to print the variance-covariance matrix of the DBT_NAm prediction stratum (deciduous broadleaf trees North America, index=6), we can use:

# index of DBT_NAm predict_stratum, idx = 6
idx = model_data_df[model_data_df['predict_stratum']=='DBT_NAm'].index.item()
# print vcov matrix
model_data['vcov'][idx]

array([[ 4.19623613, -0.30473042, -0.09762442,  0.        ,  0.        ],
       [-0.30473042,  0.05645894, -0.02532849,  0.        ,  0.        ],
       [-0.09762442, -0.02532849,  0.03291459,  0.        ,  0.        ],
       [ 0.        ,  0.        ,  0.        ,  0.        ,  0.        ],
       [ 0.        ,  0.        ,  0.        ,  0.        ,  0.        ]])

Let’s also print out the variables predictor_id, rh_index, and par for the DBT_NAm prediction stratum.

## get predictor_id, rh_index and par for idx = 6
predictor_id = model_data['predictor_id'][idx]
rh_index = model_data['rh_index'][idx]
par = model_data['par'][idx]

# print
print_s = f"""predictor_id: {predictor_id}
rh_index: {rh_index}
par: {par}"""
print(print_s)

predictor_id: [1 2 0 0 0 0 0 0]
rh_index: [50 98  0  0  0  0  0  0]
par: [-120.77709198    5.50771856    6.80801821    0.            0.        ]

The predictor_id variable gives the identifier of the predictor variable. The same consecutive predictor values indicate that the product of two metrics was used in the linear model. The variable rh_index gives the index of the relative height (RH) metrics used as predictors. For DBT_NAm stratum, two predictors RH50 and RH98 were used. The variable par gives model coefficients - the first element of the list is always the intercept of the linear model.

We can use the values from these three variables (predictor_id, rh_index, and par) to construct the linear AGBD model for each prediction strata. Refer to GEDI_L4A_Common_Queries for more information on how to assign coefficients and predictor variables to the linear models.

# initialize arrays
stratum_arr, modelname_arr, fitstratum_arr, agbd_arr = [], [], [], []
# loop the model_data_df dataframe
for idx, row in model_data_df.iterrows():
    stratum_arr.append(model_data_df['predict_stratum'][idx])
    modelname_arr.append(model_data_df['model_name'][idx])
    fitstratum_arr.append(model_data_df['fit_stratum'][idx])
    i_0 = 0
    predictor_id = model_data['predictor_id'][idx]
    rh_index = model_data['rh_index'][idx]
    par = model_data['par'][idx]
    model_str = 'AGBD = ' + str(par[0]) # intercept
    for i in predictor_id[predictor_id>0]:
        # use product of two RH metrics when consecutive
        # predictor_id have same values
        if i == i_0:
            model_str += ' x RH_' + str(rh_index[i-1])
        # adding slope coefficients
        else:
            model_str += ' + ' + str(par[i]) + ' x RH_' + str(rh_index[i-1])
        i_0 = i
    # agbd model
    agbd_arr.append(model_str)

# unique agbd models
unique_models = list(set(agbd_arr))

# printing agbd models by predict_stratum
data=[]
for model in unique_models:
    s, m, f = [], [], []
    for i, x in enumerate(agbd_arr):
        if x == model:
            s.append(stratum_arr[i])
            m.append(modelname_arr[i])
            f.append(fitstratum_arr[i])
    data.append([", ".join(s), ", ".join(list(set(m))),
                 ", ".join(list(set(f))), model])

headers = ["predict_stratum", "model_name", "fit_stratum", "AGBD model"]
df = pd.DataFrame(data, columns=headers)
tbl_n += 1
caption = f'Table {tbl_n}. AGBD Linear Models by Prediction Stratum'
df.style.set_caption(caption).hide(axis="index")

Table 3. AGBD Linear Models by Prediction Stratum

predict_stratum	model_name	fit_stratum	AGBD model
DBT_Au, EBT_Au	EBT_Au	EBT_Au	AGBD = -155.41419982910156 + 7.816701889038086 x RH_70 + 7.7095465660095215 x RH_98
DBT_Af	DBT_Af	DBT_Af	AGBD = -118.40806579589844 + 1.956794023513794 x RH_50 + 9.96180534362793 x RH_98
ENT_Au, DNT_Au	ENT_Au	ENT_Au	AGBD = -101.98419952392578 + 6.396724700927734 x RH_40 + 4.258835315704346 x RH_98
DBT_SA, EBT_SA	EBT_SA	EBT_SA	AGBD = -134.77015686035156 + 6.653591632843018 x RH_50 + 6.687118053436279 x RH_98
ENT_Af, ENT_NAs, ENT_SA, ENT_SAs, DNT_Af, DNT_NAs, DNT_SA, DNT_SAs	ENT_coarse	ENT	AGBD = -118.41133880615234 + 7.776707172393799 x RH_60 + 4.377904415130615 x RH_98
GSW_Au	GSW_Au	GSW	AGBD = -151.3834991455078 + 4.490713596343994 x RH_50 + -2.346837282180786 x RH_80 + 12.941423416137695 x RH_98
DBT_SAs, EBT_Af, EBT_SAs	EBT_coarse, EBT_Af	EBT	AGBD = -104.9654541015625 + 6.802174091339111 x RH_50 + 3.9553122520446777 x RH_98
GSW_Af, GSW_Eu, GSW_NAs, GSW_SA, GSW_SAs, GSW_NAm	GSW_coarse	GSW	AGBD = -124.83228302001953 + 12.426309585571289 x RH_98
DBT_Eu, EBT_Eu, ENT_Eu, DNT_Eu	ENT_Eu, DBT_Eu	Eu	AGBD = -96.53070068359375 + 7.175395488739014 x RH_70 + 2.9214682579040527 x RH_98
ENT_NAm, DNT_NAm	ENT_NAm	ENT	AGBD = -114.35456848144531 + 8.400657653808594 x RH_70 + 3.3459579944610596 x RH_98
DBT_NAs, EBT_NAs	DBT_coarse	DBT	AGBD = -110.05912780761719 + 5.133802890777588 x RH_60 + 6.171630382537842 x RH_98
DBT_NAm, EBT_NAm	DBT_NAm	NAm	AGBD = -120.77709197998047 + 5.507718563079834 x RH_50 + 6.808018207550049 x RH_98

As we see in the table above, some predict strata share the same AGBD model. There are a total of 12 AGBD models representing 35 prediction strata.

5. BEAM groups

GEDI instrument has two full-power lasers, each producing two beams and one coverage laser producing four beams, generating a total of 8 beams. GEDI L4A data are grouped by these beams (group name starting with BEAMXXXX). Let’s print the name and description of BEAM groups. Each of the beams is assigned beam and channel numbers.

data = []
# loop through the root groups
for v in list(hf.keys()):
    if v.startswith('BEAM'):
        beam = hf.get(v)
        b_beam = beam.get('beam')[0]
        channel = beam.get('channel')[0]
        data.append([v, hf[v].attrs['description'], b_beam, channel])

# print as a table
headers = ["beam name", "description", "beam", "channel"]
df = pd.DataFrame(data, columns=headers)
tbl_n += 1
caption = f'Table {tbl_n}. GEDI Beams'
df.style.set_caption(caption).hide(axis="index")

Table 4. GEDI Beams

beam name	description	beam	channel
BEAM0000	Coverage beam	0	0
BEAM0001	Coverage beam	1	0
BEAM0010	Coverage beam	2	1
BEAM0011	Coverage beam	3	1
BEAM0101	Full power beam	5	2
BEAM0110	Full power beam	6	3
BEAM1000	Full power beam	8	4
BEAM1011	Full power beam	11	5

Let’s look into the data structure of one of the beams, BEAM0110, a full-powered beam. All of the 8 beams have the same set of variables and variable groups.

# get BEAM0110
beam_str = 'BEAM0110'
beam0110 = hf[beam_str]

data = []

# loop over all the variables within BEAM0110 group
for v, var in beam0110.items():
    source = ''
    # if the key is a subgroup assign GROUP tag
    if isinstance(var, h5py.Group):
        data.append([v, 'GROUP', 'GROUP', 'GROUP'])
    # read source, description, units attributes of each variables
    else:
        if 'source' in var.attrs.keys():
            source = var.attrs['source']
        data.append([v, var.attrs['description'], var.attrs['units'], source])

# print all variable name and attributes as a table
headers = ["variable", "description", "units", "source"]
df = pd.DataFrame(data, columns=headers)
tbl_n += 1
caption = f'Table {tbl_n}. Variables within {beam_str} group'
df.style.set_caption(caption).hide(axis="index")

Table 5. Variables within BEAM0110 group

variable	description	units	source
agbd	Aboveground biomass density (Mg / ha)	Mg / ha
agbd_pi_lower	Lower prediction interval (see alpha attribute for the level)	Mg / ha
agbd_pi_upper	Upper prediction interval (see alpha attribute for the level)	Mg / ha
agbd_prediction	GROUP	GROUP	GROUP
agbd_se	Aboveground biomass density (Mg / ha) prediction standard error	Mg / ha
agbd_t	Model prediction in fit units	-
agbd_t_se	Model prediction standard error in fit units (needed for calculation of custom prediction intervals)	-
algorithm_run_flag	The L4A algorithm is run if this flag is set to 1. This flag selects data which have sufficient waveform fidelity for AGBD estimation.	-
beam	Beam identifier	-	L2A
channel	Channel identifier	-	L2A
degrade_flag	Flag indicating degraded state of pointing and/or positioning information	-	L2A
delta_time	Time delta since Jan 1 00:00 2018.	s	L2A
elev_lowestmode	Elevation of center of lowest mode relative to reference ellipsoid	m	L2A
geolocation	GROUP	GROUP	GROUP
l2_quality_flag	Flag identifying the most useful L2 data for biomass predictions	-
l4_quality_flag	Flag simplifying selection of most useful biomass predictions	-
land_cover_data	GROUP	GROUP	GROUP
lat_lowestmode	Latitude of center of lowest mode	degrees	L2A
lon_lowestmode	Longitude of center of lowest mode	degrees	L2A
master_frac	Master time, fractional part. master_int+master_frac is equivalent to /BEAMXXXX/delta_time.	s	L2A
master_int	Master time, integer part. Seconds since master_time_epoch. master_int+master_frac is equivalent to /BEAMXXXX/delta_time.	s	L2A
predict_stratum	Character ID of the prediction stratum name for the 1 km cell	-
predictor_limit_flag	Predictor value is outside the bounds of the training data (0=In bounds; 1=Lower bound; 2=Upper bound)	-
response_limit_flag	Prediction value is outside the bounds of the training data (0=In bounds; 1=Lower bound; 2=Upper bound)	-
selected_algorithm	selected_algorithm	-	L2A
selected_mode	ID of mode selected as lowest non-noise mode	-	L2A
selected_mode_flag	Flag indicating status of selected_mode	-	L2A
sensitivity	Maxmimum canopy cover that can be penetrated considering the SNR of the waveform	-	L2A
shot_number	Shot number	-	L2A
solar_elevation	Solar elevation angle	degrees	L2A
surface_flag	Indicates elev_lowestmode is within 300m of Digital Elevation Model (DEM) or Mean Sea Surface (MSS) elevation	-	L2A
xvar	Predictor variables (offset and transformation have been applied)	-

‘L2A’ in the ‘source’ column indicates that the variable originates from the GEDI Level 2A dataset, which provides footprint level elevation and canopy height metrics. Let’s look into each of the variables in more detail. The AGBD variables include agbd, agbd_pi_lower, agbd_pi_upper, agbd_prediction, agbd_se. The variable delta_time provides time for each shot. shot_number is a unique number assigned to each GEDI shot. Quality flags are included in l2_quality_flag and l4_quality_flag, among others. Geolocation of shots is provided in lat_lowestmode, lon_lowestmode, and elev_lowestmode. Let’s use this information to plot the path of each of the eight beams. First, let’s read the latitudes, longitudes, and time variables into a pandas dataframe.

# initialize lists
lat_l = []
lon_l = []
beam_n = []
time_l=[]

# loop over all base groups
for var in list(hf.keys()):
    if var.startswith('BEAM'):
        # reading lat, lon, time
        beam = hf.get(var)
        lat = beam.get('lat_lowestmode')[:] # latitude
        lon = beam.get('lon_lowestmode')[:] # longitude
        time = beam.get('delta_time')[:] # time
        # appending each beam into the array
        lat_l.extend(lat.tolist())
        lon_l.extend(lon.tolist())
        time_l.extend(time.tolist())
        # beam_n as a new column indicating beam number
        n = lat.shape[0] # number of shots in the beam group
        beam_n.extend(np.repeat(str(var), n).tolist())

# read the lists into a dataframe
l4adf = pd.DataFrame(list(zip(beam_n,lat_l,lon_l,time_l)), 
                     columns=["beam", "lat_lowestmode", 
                              "lon_lowestmode", "delta_time"])

# print the first few shots of the BEAM0110
l4adf[l4adf['beam']=='BEAM0110'].head()

	beam	lat_lowestmode	lon_lowestmode	delta_time
835937	BEAM0110	51.793301	15.546454	8.093945e+07
835938	BEAM0110	51.793303	15.547279	8.093945e+07
835939	BEAM0110	51.793304	15.548105	8.093945e+07
835940	BEAM0110	51.793306	15.548934	8.093945e+07
835941	BEAM0110	51.793308	15.549704	8.093945e+07

We can now plot each of the eight beams. The total number of shots (n) in each beam is shown in the parenthesis.

# first converting pandas dataframe into geopandas
l4agdf = gpd.GeoDataFrame(l4adf, crs="EPSG:4326",
                          geometry=gpd.points_from_xy(l4adf.lon_lowestmode,
                                                      l4adf.lat_lowestmode))

# plot each beam as subplot
fig, axs = plt.subplots(nrows=2, ncols=4, sharex=True, sharey=True, figsize=(14,6))
fig_n = 1 # figure number
fig.suptitle(f'Figure {fig_n}. Plots of beams for {GEDIL4A}. Color indicates `delta_time`')
axs = axs.ravel()

# loop over each beam
for i, beam in enumerate(l4adf.beam.unique()):
    subdf = l4agdf[l4agdf['beam'] == beam]
    # color the beam using delta_time
    subdf.to_crs(epsg=3857).plot(ax=axs[i],column='delta_time', 
                                 cmap='viridis', markersize=2)
    axs[i].set_title(f'{beam}, n={str(len(subdf.index))}')
    axs[i].axis('off')
    ctx.add_basemap(axs[i], source=ctx.providers.CartoDB.Positron)

plt.show()

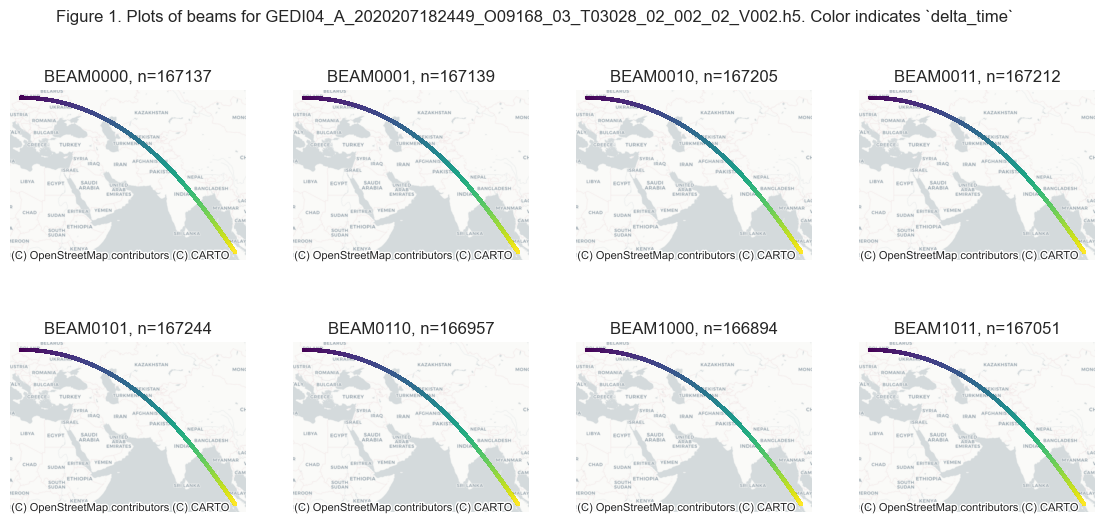
As shown in Figure 1 above, there are different numbers of shots in each beam group. The beams are usually always turned on over the land surface. This particular orbit scanned from west to east, as indicated by the delta_time variable (blue being the minimum and yellow the maximum).

The variable delta_time provides time for each shot in seconds since Jan 1 00:00 2018. We can convert the time to actual date and time using datetime module.

# datetime since
dt1 = datetime(2018, 1, 1, 0, 0, 0)
# min, max  and range datetime 
min_dt = dt1 + pd.to_timedelta(l4adf.delta_time.min(), unit='s')
max_dt = dt1 + pd.to_timedelta(l4adf.delta_time.max(), unit='s')
range_dt = max_dt - min_dt
# printing 
print_s = f"""Start time: {min_dt}
End time: {max_dt}
Total period: {range_dt}
Total shots: {len(l4adf.index)}"""
print(print_s)

Start time: 2020-07-25 19:10:52.328367
End time: 2020-07-25 19:34:02.323636
Total period: 0:23:09.995269
Total shots: 1336839

As shown above, the GEDI instrument acquired the first shot of this sub-orbit at 2020-07-25 19:10:52 and the last shot at 2020-07-25 19:34:02. In this 23 minutes period, all eight beams recorded a total of ~1.3 million shots!

To look at the spatial distribution of the GEDI shots, let’s zoom in to an area in the Mount Leuser National Park in Indonesia, where the orbit overpasses, and plot all the beams together.

# Mt Leuser Buffer of 6km
mt_leuser_gdf= gpd.GeoSeries([Point((97.1736, 3.7563))], crs="EPSG:4326")
mt_leuser_3857_gdf = mt_leuser_gdf.to_crs(epsg=3857)
mt_leuser_buffer = mt_leuser_3857_gdf.buffer(6000)

# assigning CRS of base map
l4agdf_3857 = l4agdf.to_crs(epsg=3857)
# clipping the beam_var to the buffer
leuser_gdf = l4agdf_3857[l4agdf_3857['geometry'].within(
    mt_leuser_buffer.geometry[0])]

# plotting the shots
ax = leuser_gdf.plot(alpha=0.8,  column='delta_time',
                     cmap='viridis', figsize=(7, 7))
# plotting buffer circle
mt_leuser_buffer.plot(ax=ax,color='white',
                      edgecolor='red', linewidth=5, alpha=0.4)
# plotting Mt Leuser
mt_leuser_3857_gdf.plot(ax=ax, color='red')

# Annotating Mt. Leuser
ax.annotate('MT LEUSER', xy=(mt_leuser_3857_gdf.geometry.x[0],
                             mt_leuser_3857_gdf.geometry.y[0]),
            xytext=(3, 3), textcoords="offset points", weight='bold')
j = 0
for i, beam in enumerate(l4adf.beam.unique()):
    firstrow = leuser_gdf[leuser_gdf['beam']==beam].iloc[j]
    # Annotating the beam number
    ax.annotate(str(firstrow.beam),
                xy=(firstrow.geometry.x, firstrow.geometry.y),
                arrowprops={"arrowstyle": '->'},
                xytext=(3, 10), textcoords="offset points", weight='bold')
    # display labels apart by 10
    j +=10
# scalebar
ax.add_artist(ScaleBar(1))
fig_n += 1
ax.set_title(f'Figure {fig_n}. {GEDIL4A} beams within a 6 km buffer around \
Mt Leuser, Indonesia')
#adding basemap
ctx.add_basemap(ax, source=ctx.providers.OpenTopoMap)
plt.show()

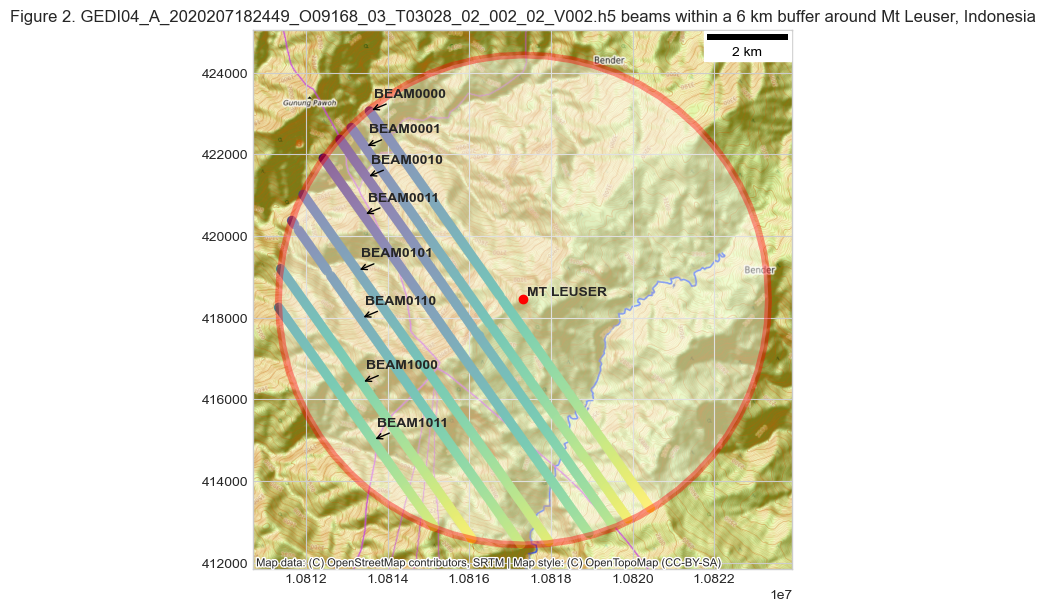
GEDI beams are ~600m apart across the track. The distance between the two outer beams is ~4.2 km.

Now, let’s look at variables within one of the beam groups, BEAM0110, in more detail. We will read all the base variables within this beam group into a pandas dataframe.

# arrays to store variable names and values
var_names = []
var_val = []
# read BEAM0110
beam0110 = hf.get('BEAM0110')
# loop through all the items in BEAM0110 and append
# to the arrays var_names, var_val
for key, value in beam0110.items():
    if not isinstance(value, h5py.Group):
         # xvar variables have 2D
        if key.startswith('xvar'):
            for r in range(4):
                var_names.append(key + '_' + str(r+1))
                var_val.append(value[:, r].tolist())
        else:
            var_names.append(key)
            var_val.append(value[:].tolist())

# create a pandas dataframe
beam_df = pd.DataFrame(map(list, zip(*var_val)), columns=var_names)
# set shot_number as dataframe index
beam_df = beam_df.set_index('shot_number')

Now, the beam_df dataframe contains all the variables within the BEAM0110 group. Let’s convert it to a geopandas dataframe to assign spatial context.

# convert to a geopandas dataframe for plotting
beam_gdf = gpd.GeoDataFrame(beam_df,
                            geometry=gpd.points_from_xy(beam_df.lon_lowestmode,
                                                        beam_df.lat_lowestmode))
# assigning CRS of WGS84
beam_gdf.crs = "EPSG:4326"
# turning fill values (-9999) to nan
beam_gdf = beam_gdf.replace(-9999, np.nan)

5.1 Prediction Stratum

Let’s compute percent shots by the predict_stratum variable for the BEAM0110.

# percent shots in each predict_stratum
predict_stratum=beam_gdf.predict_stratum.str.decode(
    'utf-8').value_counts(normalize=True).mul(100).round(3)
# plotting the values as bar diagram
ax = predict_stratum.plot(kind='bar', figsize=(20, 4))
ax.legend(["percent shots"])
fig_n += 1
ax.set_title(f'Figure {fig_n}. Percent shots by predict_stratum in {beam0110.name} \
of {GEDIL4A}')
# displaying values for each bar
for container in ax.containers:
    ax.bar_label(container)
plt.show()

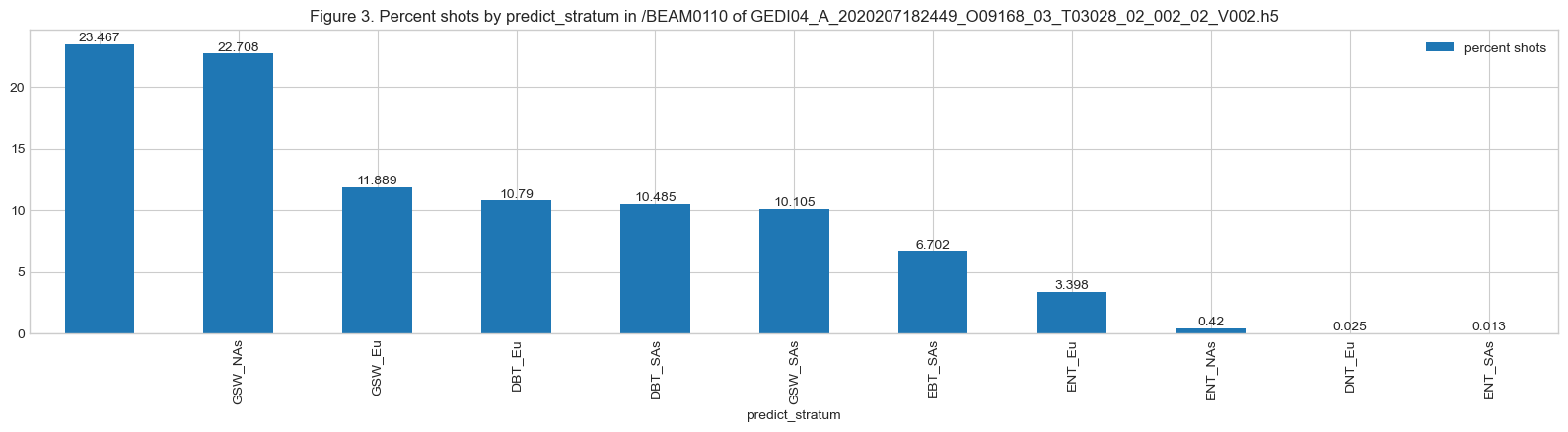
This particular suborbit passes through 10 different prediction strata, as shown in Figure 3, covering several forest regions. About 23% of the total shots have no prediction stratum assigned and are not in one of the 35 GEDI predict strata (e.g., water).

There are three sub-groups within each beam group indicated by ‘GROUP’ in Table 5 above - agbd_prediction, geolocation, and land_cover_data.

6. Land Cover Group

The group land_cover_data within the beam group contains land cover information for the GEDI shots. Let’s read all the variables within the \BEAM0110\land_cover_data group.

var_names = []
var_val = []
data = []

# loop through all variables within land_cover_data subgroup
for key, value in beam0110['land_cover_data'].items():
    var_names.append(key)
    var_val.append(value[:].tolist())
    data.append([key, value.attrs['description'], value.attrs['units']])

# create a pandas dataframe        
beam_lc_df = pd.DataFrame(map(list, zip(*var_val)), columns=var_names)
beam_lc_df = beam_lc_df.set_index('shot_number')

# join with the previous dataframe conaining root variables
# pandas will use `shot_number` as a common index to join
beam_gdf = beam_gdf.join(beam_lc_df)

# print variable description as table
headers = ["variable", "description", "units"]
df = pd.DataFrame(data, columns=headers)
tbl_n += 1
caption = f'Table {tbl_n}. Variables within land_cover_data group'
df.style.set_caption(caption).hide(axis="index")

Table 6. Variables within land_cover_data group

variable	description	units
landsat_treecover	Tree cover in the year 2010, defined as canopy closure for all vegetation taller than 5m in height (Hansen et al.). Encoded as a percentage per output grid cell.	percent
landsat_water_persistence	The percent UMD GLAD Landsat observations with classified surface water between 2018 and 2019. Values > 80 usually represent permanent water while values < 10 represent permanent land.	percent
leaf_off_doy	GEDI 1 km EASE 2.0 grid leaf-off start day-of-year derived from the NPP VIIRS Global Land Surface Phenology Product.	days
leaf_off_flag	GEDI 1 km EASE 2.0 grid flag derived from leaf_off_doy, leaf_on_doy and pft_class, indicating if the observation was recorded during leaf-off conditions in deciduous needleleaf or broadleaf forests and woodlands. 1 = leaf-off and 0 = leaf-on.	-
leaf_on_cycle	Flag that indicates the vegetation growing cycle for leaf-on observations. Values are 0 (leaf-off conditions), 1 (cycle 1) or 2 (cycle 2).	-
leaf_on_doy	GEDI 1 km EASE 2.0 grid leaf-on start day-of-year derived from the NPP VIIRS Global Land Surface Phenology Product.	-
pft_class	GEDI 1 km EASE 2.0 grid Plant Functional Type (PFT) derived from the MODIS MCD12Q1v006 Product. Values follow the Land Cover Type 5 Classification scheme.	-
region_class	GEDI 1 km EASE 2.0 grid world continental regions (0: Water, 1: Europe, 2: North Asia, 3: Australasia, 4: Africa, 5: South Asia, 6: South America, 7: North America).	-
shot_number	Shot number	-
urban_focal_window_size	The focal window size used to calculate urban_proportion. Values are 3 (3x3 pixel window size) or 5 (5x5 pixel window size).	pixels
urban_proportion	The percentage proportion of land area within a focal area surrounding each shot that is urban land cover. Urban land cover is derived from the DLR 12 m resolution TanDEM-X Global Urban Footprint Product.	percent

Let’s look at some key variables in more detail.

6.1 Plant Functional Types

The pft_class variable provides the plant functional types for the shots, which are derived from the MODIS land cover type product (MCD12Q1). It uses LC_Type5 or Annual PFT classification. Please refer to Table 7 of the MCD12Q1 user guide for the PFT type legend. Let’s plot distribution of shots by PFT class for the BEAM0110.

# percentage of shots by pft_class
pft_class=beam_gdf.pft_class.value_counts(normalize=True).mul(100).round(3).sort_index()

# MCD12Q1 PFT types
pft_legend = {'Water Bodies': 0, 'Evergreen Needleleaf Trees': 1,
              'Evergreen Broadleaf Trees': 2, 'Deciduous Needleleaf Trees': 3, 
              'Deciduous Broadleaf Trees': 4, 'Shrub': 5, 'Grass': 6,
              'Cereal Croplands': 7, 'Broadleaf Croplands': 8, 
              'Urban and Built-up Lands': 9, 
              'Permanent Snow and Ice': 10, 'Barren' : 11, 
              'Unclassified': 255}
# get color from tab20
cmap = colormaps.get_cmap('tab20')
patchList = []
tab20 = []
# creating a legend
for key, i in pft_legend.items():
    label = f'{key} [{str(i)}] - {pft_class.get(i, 0)}%'
    data_key = Line2D([0], [0], marker='o', color='w', label=label,
                          markerfacecolor=cmap(i), markersize=8)
    tab20.append(cmap(i))
    patchList.append(data_key)
newcmp = ListedColormap(tab20)

ax=beam_gdf.to_crs(epsg=3857).plot(column='pft_class', alpha=0.8,
                                   categorical=True, cmap=newcmp,
                                   legend_kwds={'facecolor': 'lightgray',
                                                'framealpha': 1},
                                   figsize=(12, 7), markersize=3, legend=True)
fig_n += 1
ax.set_title(f'Figure {fig_n}. Distribution of shots by PFT class in {beam0110.name} \
of {GEDIL4A}')
ctx.add_basemap(ax, source=ctx.providers.CartoDB.Positron)
ax.legend(handles=patchList, bbox_to_anchor=(1, 1), loc='upper left')
plt.show()

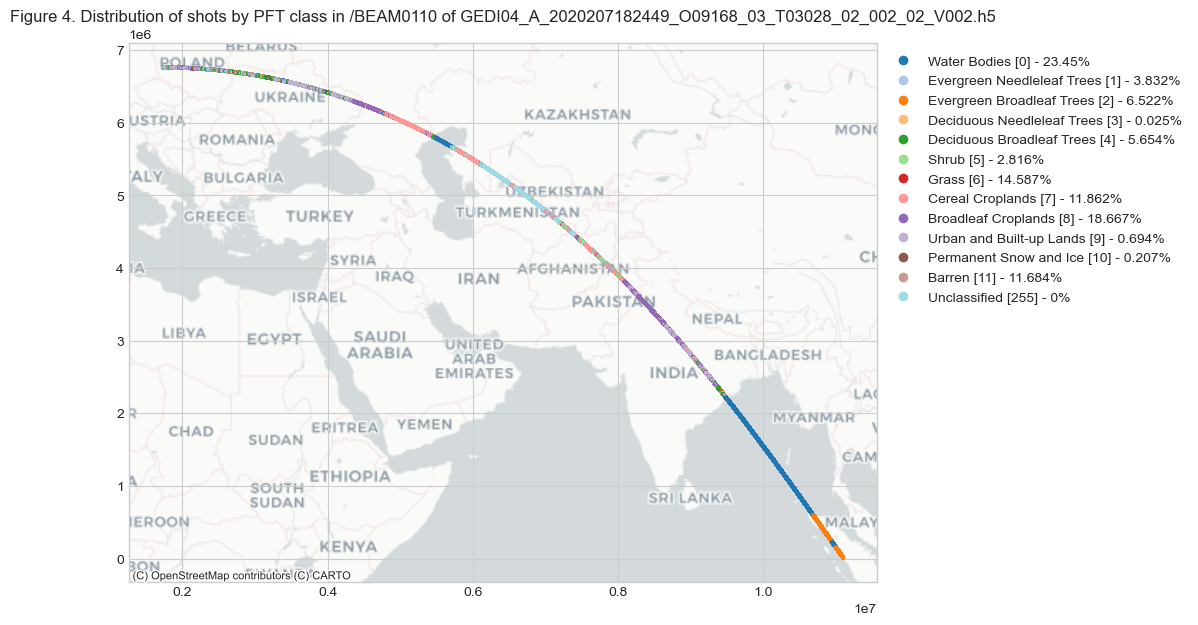
As we noted earlier (Figures 3 and 4), water bodies constitute ~23% of the total shots.

6.2 Urban Proportion

Another variable of interest is urban_proportion, which provides the proportion of urban land cover within the search area defined by urban_focal_window_size variable. The window size is defined as the number of pixels in the 25 m global urban mask developed by the GEDI science team using the TerraSAR-X and TanDEMX global urban footprint data products.

# subsetting the shots with urban cover > 50%
beam_urban_gdf = beam_gdf[beam_gdf['urban_proportion'] > 50]

ax = beam_gdf[beam_gdf['urban_proportion'] <= 50].to_crs(epsg=3857).plot(
    color='grey', alpha=0.01, markersize=2, linewidth=0, figsize=(12, 7))
beam_urban_gdf.to_crs(epsg=3857).plot(ax=ax,column='urban_proportion',
                                      alpha=0.4, cmap='seismic',
                                      markersize=4, legend=True,
                                      legend_kwds={'label': 'Urban Land Cover (%)'})

# figure title
n_urban = len(beam_urban_gdf.index)
percent_urban = (n_urban/len(beam_gdf.index)) * 100
fig_n += 1
ax.set_title(f'''Figure {fig_n}. Shots with proportion of urban land cover \
> 50% in {beam0110.name} of {GEDIL4A},
n = {len(beam_urban_gdf.index)} ({round(percent_urban,3)}%) total shots''')
ctx.add_basemap(ax, source=ctx.providers.CartoDB.Positron)
plt.show()

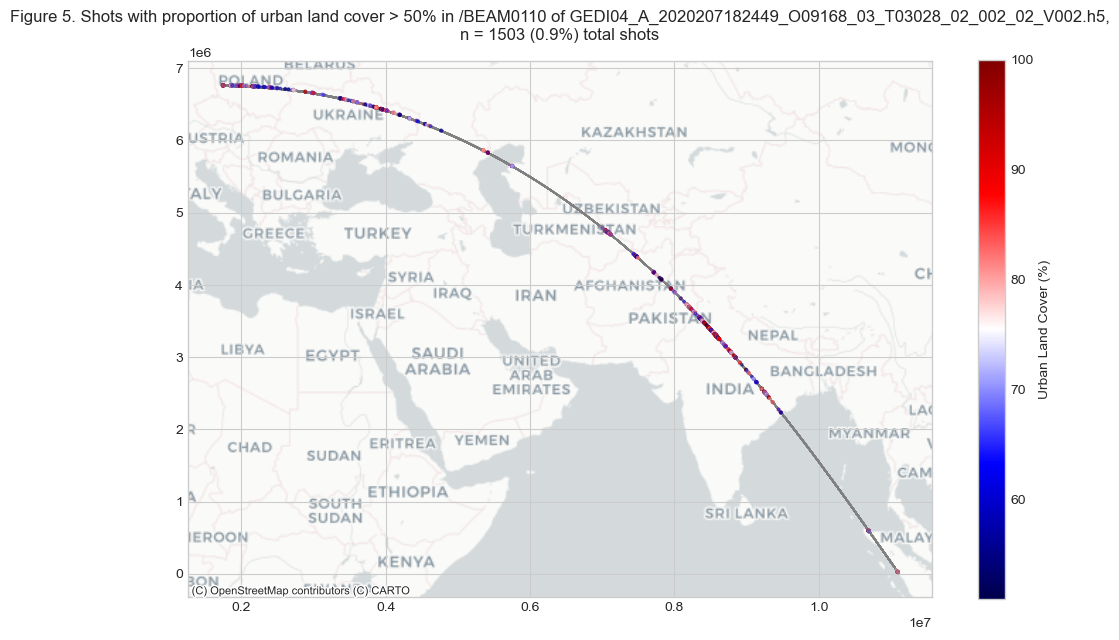
As shown in Figure 5, 0.9% of the total GEDI BEAM0110 shots falls over the urban areas (>50% urban cover). The shots with <=50% urban land cover is shown in the grey color.

6.3 Phenology

GEDI L4A footprints include phenology information derived from VIIRS/S-NPP Land Surface Phenology VNP22Q2 in the variables leaf_on_doy, leaf_off_doy and leaf_on_cycle. These variables together with the PFT are used to indicate whether the GEDI shots were recorded during the leaf-off or leaf-on conditions, provided in the leaf_off_flag. When the shot is collected after the onset of maximum greenness and before the midpoint of the senescence phase, they are marked with a flag of 1 (leaf-off).

Let’s plot the leaf_off_flag on a map.

# plotting leaf-on as grey
ax = beam_gdf[beam_gdf['leaf_off_flag']==0].to_crs(epsg=3857).plot(
    color='grey', alpha=0.01, linewidth=0, markersize=2, figsize=(12, 7))
# plotting leaf-off as red
leaf_on_gdf =beam_gdf[beam_gdf['leaf_off_flag']==1]
leaf_on_gdf.to_crs(epsg=3857).plot(ax=ax, color='red', alpha=0.4, markersize=4)

# getting counts by pft_class
leaf_off=leaf_on_gdf.pft_class.value_counts()
# total shots with leaf-off
n_leaf_off = leaf_off.sum()
# pft classes of leaf-off shots
pft_leaf_off = ",".join([list(pft_legend.keys())[i] for i,v in leaf_off.items()])
# percent leaf off
percent_leaf_off = (n_leaf_off/len(beam_gdf.index)) * 100

# figure title
fig_n += 1
ax.set_title(f'''Figure {fig_n}. Leaf off shots indicated by red color {beam0110.name}\
of {GEDIL4A}, 
n = {n_leaf_off} ({round(percent_leaf_off,3)}%) total shots in {pft_leaf_off} PFT''')
ctx.add_basemap(ax, source=ctx.providers.CartoDB.Positron)
plt.show()

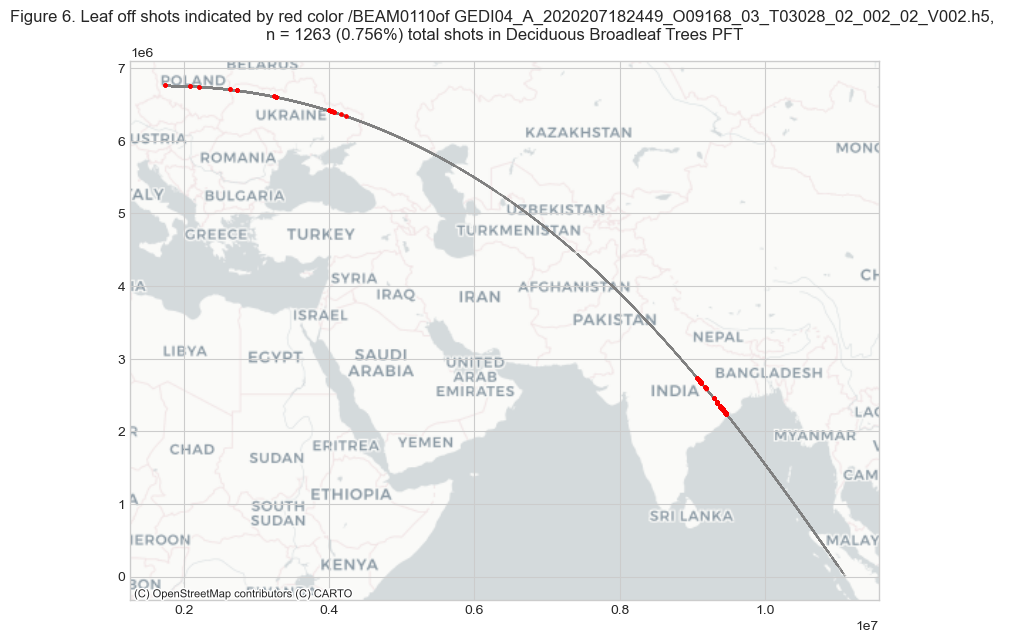
In Figure 6 above, the leaf-off shots are indicated with red. The GEDI orbit was collected on July 25, 2020. There were only 1263 shots with leaf-off conditions, all within the Deciduous Broadleaf Trees PFT.

6.4 Tree Cover

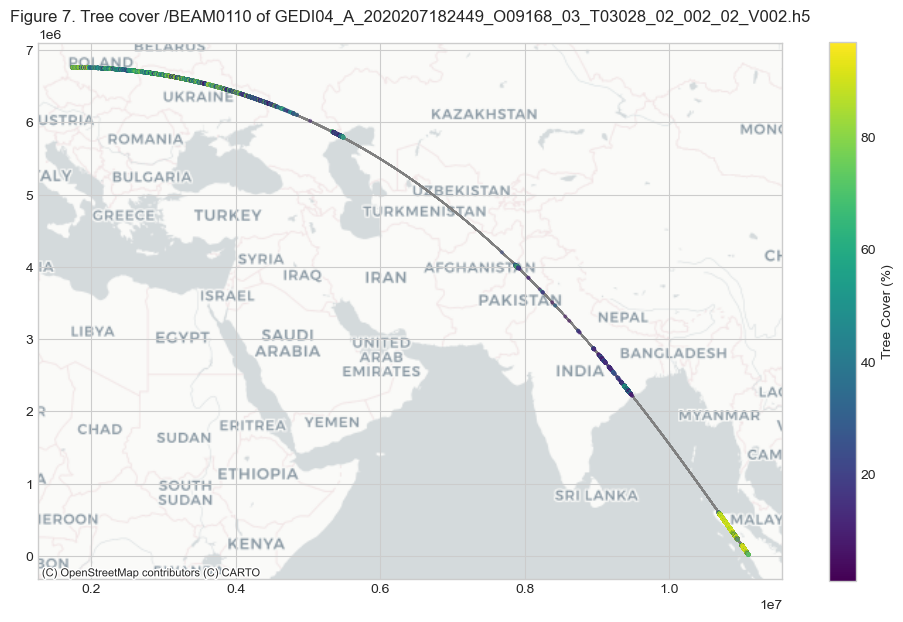
GEDI uses Landsat-derived tree cover, which is defined as canopy closure for all vegetation taller than 5 m in height (Hansen et al., 2013). The following Figure 7 shows the percent tree cover.

ax = beam_gdf.to_crs(epsg=3857).plot(color='grey', alpha=0.01,
                                     linewidth=0, markersize=2, figsize=(12, 7))
beam_gdf[beam_gdf['landsat_treecover']!=0].to_crs(epsg=3857).plot(
    ax=ax, column='landsat_treecover', cmap='viridis', alpha=0.4,
    markersize=4, legend=True, legend_kwds={'label': 'Tree Cover (%)'})

# figure title
fig_n += 1
ax.set_title(f'''Figure {fig_n}. Tree cover {beam0110.name} of {GEDIL4A}''')
ctx.add_basemap(ax, source=ctx.providers.CartoDB.Positron)
plt.show()

7. Geolocation Group

The geolocation subgroup within the BEAM group contains elevation, latitude, and longitude of the lowest mode for each of the seven algorithm settings groups. Canopy height metrics are computed relative to the elevation of the lowest mode or the last mode of the GEDI waveform. GEDI uses six different algorithm settings (a1 to a6) for webform processing (refer to the GEDI L1/L2 Waveform Processing ATBD, Table 5 for more details). Additional algorithm settings of a10 in GEDI L4A indicate that a5 has been used, but the lowest detected mode is likely noise. When this occurs, a higher mode was used to calculate RH metrics (see GEDI L4A ATBD for details).

The geolocation subgroup also provides a beam sensitivity metric for each of the seven algorithm settings. The sensitivity indicates signal strength of the GEDI shot to penetrate canopies and detect the true ground level. The subgroup also includes stale_return_flag (0=good) to indicate the signal quality.

Let’s read all the variables within the \BEAM0110\geolocation group.

var_names = []
var_val = []
data = []

# loop through all variables within land_cover_data subgroup
for key, value in beam0110['geolocation'].items():
    var_names.append(key)
    var_val.append(value[:].tolist())
    data.append([key, value.attrs['description'], value.attrs['units'],
                 value.attrs['source']])

# create a pandas dataframe        
beam_geo_df = pd.DataFrame(map(list, zip(*var_val)), columns=var_names)
beam_geo_df = beam_geo_df.set_index('shot_number')

# join with the previous dataframe conaining root variables
# pandas will use `shot_number` as a common index to join
beam_gdf = beam_gdf.join(beam_geo_df)

# print variable description as table
headers = ["variable", "description", "units", "source"]
df = pd.DataFrame(data, columns=headers)
tbl_n += 1
caption = f'Table {tbl_n}. Variables within geolocation group'
df.style.set_caption(caption).hide(axis="index")

Table 7. Variables within geolocation group

variable	description	units	source
elev_lowestmode_a1	Elevation of center of lowest mode relative to reference ellipsoid	m	L2A
elev_lowestmode_a10	Elevation of center of lowest mode relative to reference ellipsoid	m	L2A
elev_lowestmode_a2	Elevation of center of lowest mode relative to reference ellipsoid	m	L2A
elev_lowestmode_a3	Elevation of center of lowest mode relative to reference ellipsoid	m	L2A
elev_lowestmode_a4	Elevation of center of lowest mode relative to reference ellipsoid	m	L2A
elev_lowestmode_a5	Elevation of center of lowest mode relative to reference ellipsoid	m	L2A
elev_lowestmode_a6	Elevation of center of lowest mode relative to reference ellipsoid	m	L2A
lat_lowestmode_a1	Latitude of center of lowest mode	degrees	L2A
lat_lowestmode_a10	Latitude of center of lowest mode	degrees	L2A
lat_lowestmode_a2	Latitude of center of lowest mode	degrees	L2A
lat_lowestmode_a3	Latitude of center of lowest mode	degrees	L2A
lat_lowestmode_a4	Latitude of center of lowest mode	degrees	L2A
lat_lowestmode_a5	Latitude of center of lowest mode	degrees	L2A
lat_lowestmode_a6	Latitude of center of lowest mode	degrees	L2A
lon_lowestmode_a1	Longitude of center of lowest mode	degrees	L2A
lon_lowestmode_a10	Longitude of center of lowest mode	degrees	L2A
lon_lowestmode_a2	Longitude of center of lowest mode	degrees	L2A
lon_lowestmode_a3	Longitude of center of lowest mode	degrees	L2A
lon_lowestmode_a4	Longitude of center of lowest mode	degrees	L2A
lon_lowestmode_a5	Longitude of center of lowest mode	degrees	L2A
lon_lowestmode_a6	Longitude of center of lowest mode	degrees	L2A
sensitivity_a1	Maxmimum canopy cover that can be penetrated considering the SNR of the waveform	-	L2A
sensitivity_a10	Maxmimum canopy cover that can be penetrated considering the SNR of the waveform	-	L2A
sensitivity_a2	Maxmimum canopy cover that can be penetrated considering the SNR of the waveform	-	L2A
sensitivity_a3	Maxmimum canopy cover that can be penetrated considering the SNR of the waveform	-	L2A
sensitivity_a4	Maxmimum canopy cover that can be penetrated considering the SNR of the waveform	-	L2A
sensitivity_a5	Maxmimum canopy cover that can be penetrated considering the SNR of the waveform	-	L2A
sensitivity_a6	Maxmimum canopy cover that can be penetrated considering the SNR of the waveform	-	L2A
shot_number	Shot number	-	L2A
stale_return_flag	Flag from digitizer indicating the real-time pulse detection algorithm did not detect a return signal above its detection threshold within the entire 10 km search window. The pulse location of the previous shot was used to select the telemetered waveform.	-	L2A

8. AGBD variables

The agbd variable within the BEAM group contains estimated aboveground biomass density. Before looking further into agbd variables, let’s go and read in the variables agbd_prediction subgroup. The agbd_prediction subgroup contains AGBD variables for all 7 algorithm settings groups (see Section 7 above).

var_names = []
var_val = []

# loop through all variables within agbd_prediction subgroup
for key, value in beam0110['agbd_prediction'].items():
    # xvar variables have 2D
    if key.startswith('xvar'):
        for r in range(4):
            var_names.append(key + '_' + str(r+1))
            var_val.append(value[:, r].tolist())
    else:
        var_names.append(key)
        var_val.append(value[:].tolist())

# create a pandas dataframe
beam_agbd_df = pd.DataFrame(map(list, zip(*var_val)), columns=var_names)
beam_agbd_df = beam_agbd_df.set_index('shot_number')

# join with the previous dataframe conaining root variables
# pandas will use `shot_number` as a common index to join
beam_gdf = beam_gdf.join(beam_agbd_df)

The agbd_prediction subgroup contains additional important prediction parameters used. Let’s print the attributes and the values.

data = []
agbd_prediction = beam0110['agbd_prediction']
# loop through attributes
for attr in agbd_prediction.attrs.keys():
    data.append([attr, agbd_prediction.attrs[attr]])
# print attributes and values as table
headers = ["Attributes", "value"]
df = pd.DataFrame(data, columns=headers)
tbl_n += 1
caption = f'Table {tbl_n}. AGBD Prediction Attributes'
df.style.set_caption(caption).hide(axis="index")

Table 8. AGBD Prediction Attributes

Attributes	value
alpha	0.100000
l2a_alg_count	7.000000
max_nvar	4.000000
pft_grid_version	4.000000
pft_infilled_grid_version	6.000000
phenology_grid_version	5.000000
predictor_offset	100.000000
region_grid_version	5.000000
response_offset	0.000000
urban_grid_version	1.000000
water_grid_version	1.000000

In the table above, predictor_offset and response_offset are the offset appplied to predictors and response variables before fitting the AGBD model. The variable alpha is the alpha value used for calculation of prediction intervals. The AGBD models currently have maximum number of 4 predictors (max_nvar) and 7 algorithm settings groups (l2a_alg_count).

Now, let’s plot the agbd variable for the BEAM0110 along the longitude axis.

# compute bounds of beam_gdf
minx, miny, maxx, maxy = beam_gdf.total_bounds

# x, y labels
ylabel = f"{beam0110['agbd'].attrs['long_name']} ({beam0110['agbd'].attrs['units']})"

xlabel = beam0110['lon_lowestmode'].attrs['long_name']

# subset where agbd is not null (-9999)
agbd_gdf = beam_gdf[~beam_gdf['agbd'].isnull()]

# plot
percent_agbd = (len(agbd_gdf.index)/len(beam_gdf.index))*100
ax = agbd_gdf.plot.scatter(x =['lon_lowestmode'], y=['agbd'],  cmap='viridis',
                           c='agbd', alpha=0.1, ylabel=ylabel, xlabel=xlabel,
                           figsize=(20, 7), grid=True, legend=False)
fig_n += 1
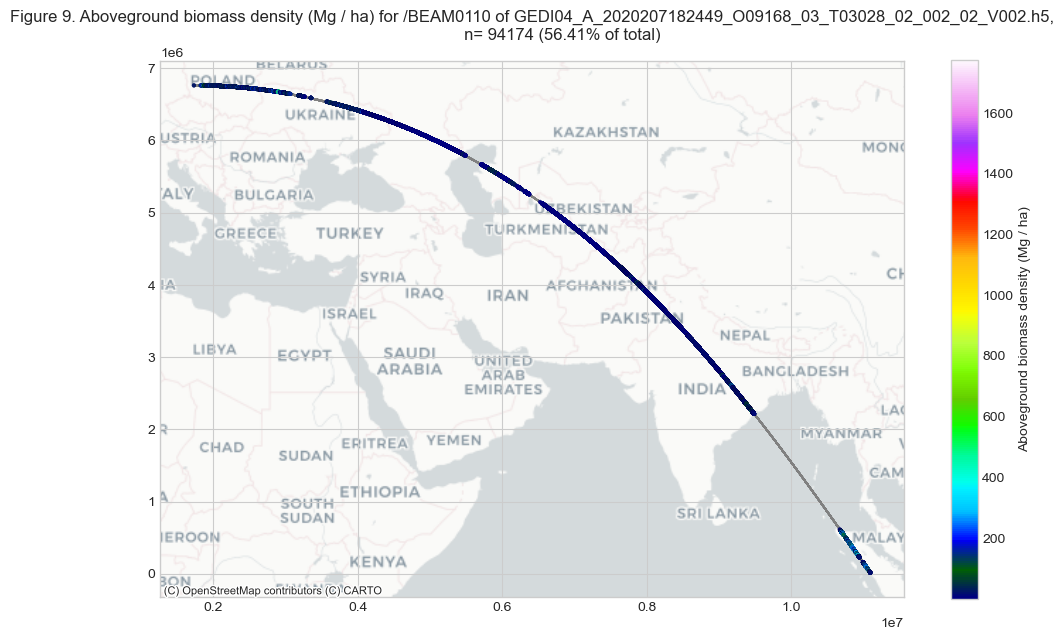
ax.set_title(f'''Figure {fig_n}. {ylabel} for {beam0110.name} of {GEDIL4A},
             n= {len(agbd_gdf.index)} ({round(percent_agbd,2)}% of total)''')
plt.show()

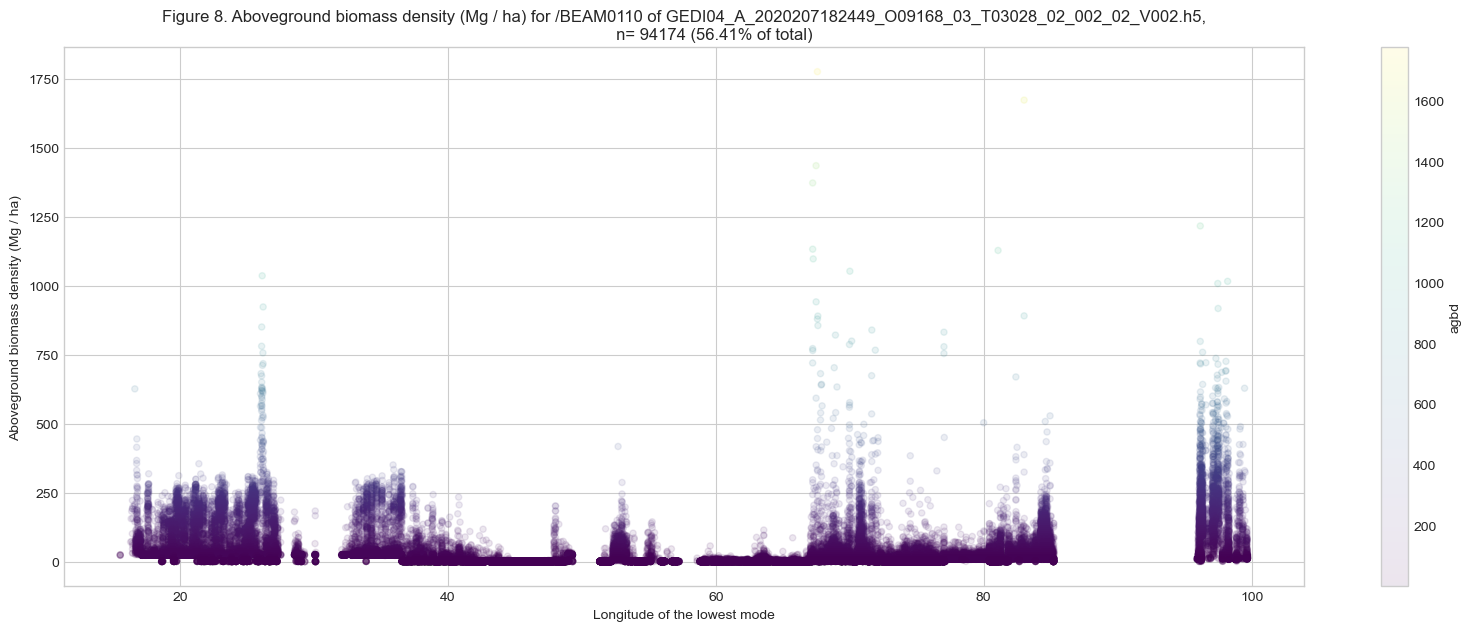
As shown in Figure 8 above, ~56% of the shots in BEAM0110 have agbd values. The shots over water surface and areas with no vegetation have no agbd values and are indicated with fill values of -9999.

Let’s also plot the agbd on a map. In the map below, the shots with no agbd values are indicated with grey dots.

ax = beam_gdf[beam_gdf['agbd'].isnull()].to_crs(epsg=3857).plot(
    color='grey', alpha=0.01, linewidth=0, markersize=2, figsize=(12, 7))
beam_gdf.to_crs(epsg=3857).plot(ax=ax, column='agbd', cmap='gist_ncar',
                                alpha=0.4, markersize=4,
                                legend=True, legend_kwds={'label': ylabel})

fig_n += 1
ax.set_title(f'''Figure {fig_n}. {ylabel} for {beam0110.name} of {GEDIL4A},
             n= {len(agbd_gdf.index)} ({round(percent_agbd,2)}% of total)''')
ctx.add_basemap(ax, source=ctx.providers.CartoDB.Positron)
plt.show()

Plotting thousands of shots from the BEAM0110 in one figure may not show the variability in details. Let’s subset the data into a smaller area for a closer look. We will subset an area in the Mount Leuser National Park in Indonesia, where the GEDI orbit overpasses. We will clip around 6 km from Mt. Leuser.

# Mt Leuser Buffer of 5km
mt_leuser_gdf= gpd.GeoSeries([Point((97.1736, 3.7563))])
mt_leuser_gdf.crs = "EPSG:4326"
mt_leuser_3857_gdf = mt_leuser_gdf.to_crs(epsg=3857)
mt_leuser_buffer = mt_leuser_3857_gdf.buffer(6000)

# assigning CRS of base map
beam_gdf_3857 = beam_gdf.to_crs(epsg=3857)
# clipping the beam_var to the buffer
leuser_gdf = beam_gdf_3857[beam_gdf_3857['geometry'].within(
    mt_leuser_buffer.geometry[0])]
# plotting first few lines
leuser_gdf.head()

	agbd	agbd_pi_lower	agbd_pi_upper	agbd_se	agbd_t	agbd_t_se	algorithm_run_flag	beam	channel	degrade_flag	...	xvar_a4_3	xvar_a4_4	xvar_a5_1	xvar_a5_2	xvar_a5_3	xvar_a5_4	xvar_a6_1	xvar_a6_2	xvar_a6_3	xvar_a6_4
shot_number
91680600300633705	NaN	NaN	NaN	NaN	NaN	NaN	0	6	3	30	...	-9999.0	-9999.0	-9999.000000	-9999.000000	-9999.0	-9999.0	-9999.000000	-9999.000000	-9999.0	-9999.0
91680600300633706	NaN	NaN	NaN	NaN	NaN	NaN	0	6	3	30	...	-9999.0	-9999.0	-9999.000000	-9999.000000	-9999.0	-9999.0	-9999.000000	-9999.000000	-9999.0	-9999.0
91680600300633707	55.617771	0.421164	203.532837	17.128305	7.067859	3.922277	1	6	3	30	...	0.0	0.0	10.310674	10.592922	0.0	0.0	10.057336	10.298059	0.0	0.0
91680600300633708	187.650787	47.486774	420.499054	17.121983	12.982439	3.921553	1	6	3	30	...	0.0	0.0	10.689247	11.437220	0.0	0.0	10.441743	11.184812	0.0	0.0
91680600300633709	255.015137	83.940132	518.769043	17.120995	15.134360	3.921440	1	6	3	30	...	0.0	0.0	10.914211	11.594396	0.0	0.0	10.296116	10.914211	0.0	0.0

5 rows × 204 columns

The geopandas dataframe leuser_gdf contains all the variables within BEAM0110 group for an area of 6 km around Mt. Leuser. Let’s plot the shots on a map.

# plotting the shots
ax = leuser_gdf.plot(alpha=0.8,  column='delta_time', cmap='viridis',
                     figsize=(8, 8))
# plotting buffer circle
mt_leuser_buffer.plot(ax=ax,color='white', edgecolor='red',
                      linewidth=5, alpha=0.4)
# plotting Mt Leuser
mt_leuser_3857_gdf.plot(ax=ax, color='red')

# Annotating Mt. Leuser
ax.annotate('MT LEUSER', xy=(mt_leuser_3857_gdf.geometry.x[0],
                             mt_leuser_3857_gdf.geometry.y[0]),
            xytext=(3, 3), textcoords="offset points", weight='bold')
# Annotating the first shot_number
ax.annotate('shot_number: '+ str(leuser_gdf.iloc[0].name),
            xy=(leuser_gdf.iloc[0].geometry.x, leuser_gdf.iloc[0].geometry.y),
            xytext=(3, 3), textcoords="offset points", weight='bold')
# Annotating the last shot_number
ax.annotate('shot_number: '+ str(leuser_gdf.iloc[-1].name),
            xy=(leuser_gdf.iloc[-1].geometry.x, leuser_gdf.iloc[-1].geometry.y),
            xytext=(3, 3), textcoords="offset points", weight='bold')
# scalebar
ax.add_artist(ScaleBar(1))

# number modulus 100000000 gives last eight digits for shot number
# computing difference between the first and the last shot numbers
total_shots = ((abs(leuser_gdf.iloc[-1].name) % 100000000) -
               (abs(leuser_gdf.iloc[0].name) % 100000000))
# figure title
fig_n += 1
ax.set_title(f'''
Figure {fig_n}. GEDI L4A {GEDIL4A} beam {beam0110.name} within a buffer \
of 6 km around Mt Leuser, Indonesia. n = {total_shots+1}
''')

#adding basemap
ctx.add_basemap(ax, source=ctx.providers.OpenTopoMap)
plt.show()

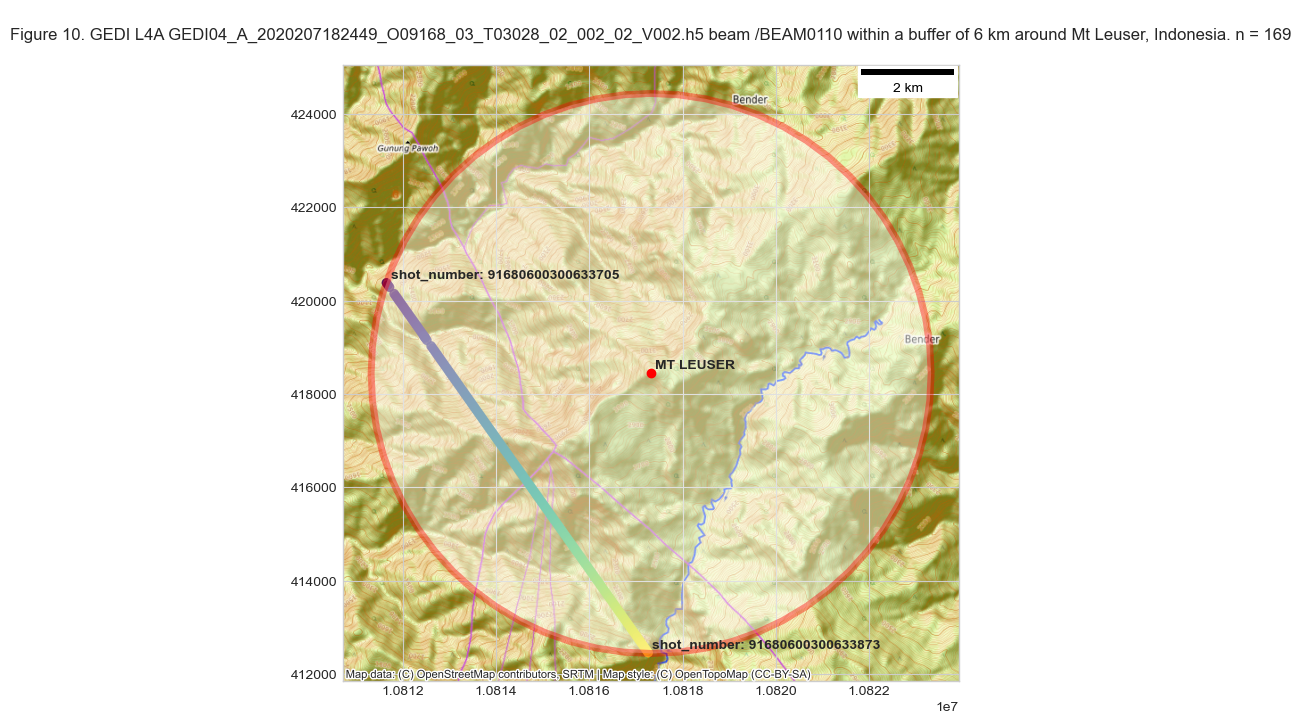
The start and end shot numbers are also shown on the map. GEDI shot numbers are 18 characters and in the format OOOOOBBFFFNNNNNNNN, where:

• OOOOO: Orbit number

• BB: Beam number

• RR: Reserved for future use

• G: Sub-orbit granule number

• NNNNNNNN: Shot index

In Figure 10 above, the start shot has a value of 091680600300633705, which means it is from the orbit number 09168, the beam number 06, the sub-orbit granule number of 3 and the shot index of 00633705 within the orbit. There are a total of 169 shots from beam 06 (or BEAM0110) within 6km of Mt. Leuser.

Now, let’s plot the AGBD variables.

# compute the distance from the first point
leuser_gdf = leuser_gdf.assign(distance=leuser_gdf.geometry.distance(
    leuser_gdf.iloc[0].geometry).values)

## x, y labels
ylabel = f"{beam0110['agbd'].attrs['long_name']} ({beam0110['agbd'].attrs['units']})"
xlabel = 'Distance in m'

# plotting agbd
ax = leuser_gdf.plot.scatter(x ='distance', y='agbd', s=15, ylabel=ylabel,
                             xlabel=xlabel, figsize=(20, 8), grid=True,
                             color='black', label="agbd")
# figure title
fig_n += 1
ax.set_title(f'''
Figure {fig_n}. {ylabel} near Mt. Leuser, Indonesia for {beam0110.name} of {GEDIL4A} \
(n= {str(len(leuser_gdf.index))}, {len(leuser_gdf[leuser_gdf['agbd'].isnull()].index)} with agbd fill values)
''')

# getting alpha attribute from the agbd_prediction group
alpha =  beam0110['agbd_prediction'].attrs['alpha']
# plotting agbd_pi_upper/lower as fill area
ax.fill_between(leuser_gdf['distance'], leuser_gdf['agbd_pi_lower'],
                leuser_gdf['agbd_pi_upper'], alpha=0.1, color='green',
                label=f"agbd prediction interval, alpha={alpha})" )
ax.legend()
plt.show()

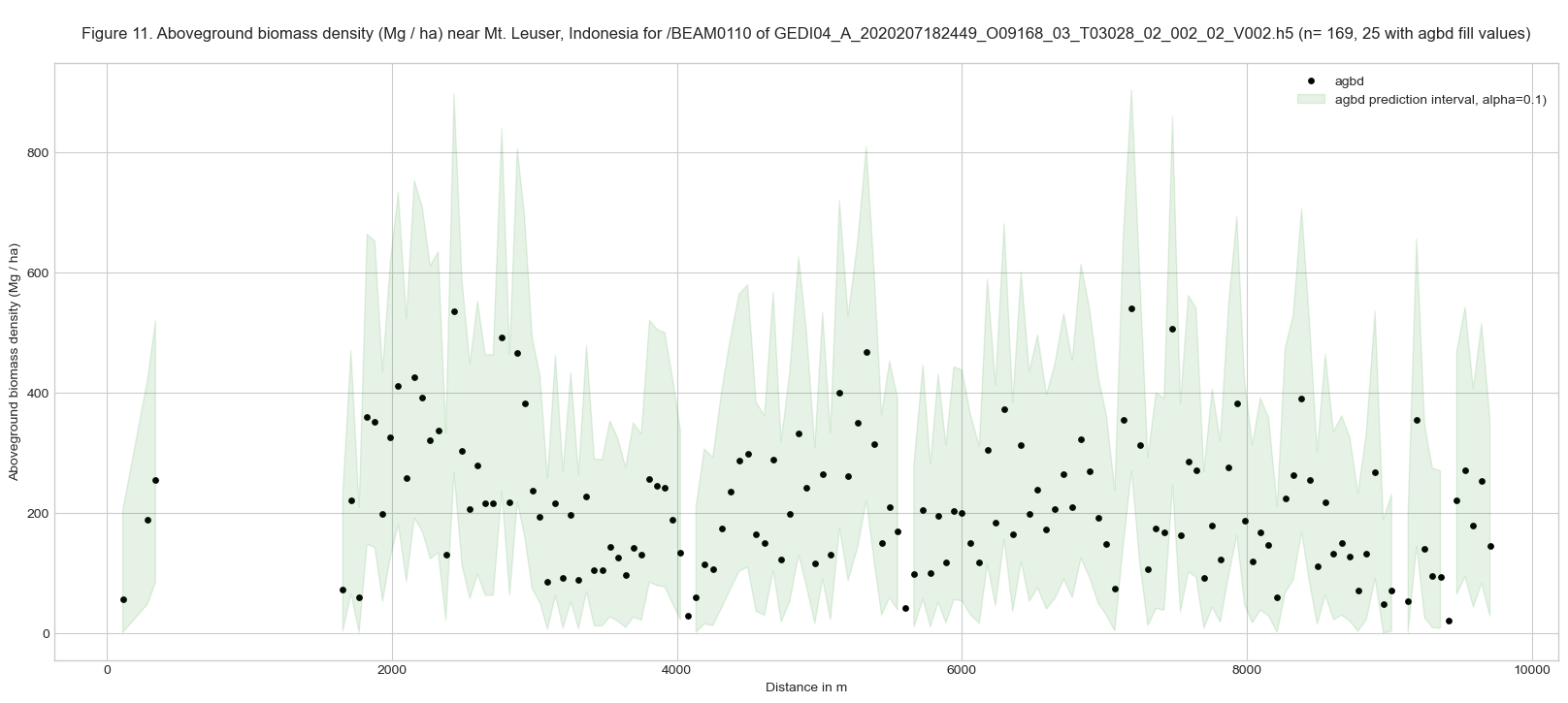
The agbd shows the selected aboveground biomass density, shown by black dots in Figure 11 above. The upper and lower prediction intervals are shown with a green-filled area.

GEDI shots are ~60m apart along the track. In the figure above, there are ~16-17 shots (shown by dots) within a distance of 1000 m. Note that a total of 25 shots with agbd fill values (-9999) are not plotted.

The above plot shows the AGBD estimates at alpha=0.1 (90% confidence interval), the default confidence interval used for these variables. To compute the estimates at a different confidence interval (e.g., 95%), we can use agbd_t and agbd_t_se variables, which provides the prediction in transform space. For more details, please refer to GEDI L4A Common Queries.

# 99% confidence interval
alpha_2 = 0.01
# degree of freedom for shots

leuser_gdf['predict_stratum'] = leuser_gdf['predict_stratum'].str.decode('utf-8')
for i, row in leuser_gdf.iterrows():
    # model_data_df dataframe from Section 4 above contains ancillary variables
    midx = model_data_df['predict_stratum']==row['predict_stratum']
    dof = model_data_df[midx].dof.item()
    bias = model_data_df[midx].bias_correction_value.item()
    leuser_gdf.at[i,'dof']=dof
    leuser_gdf.at[i,'bias_correction_value']=bias

tse = leuser_gdf['agbd_t_se'] * stats.t.ppf(1-(alpha_2/2), leuser_gdf['dof'])
leuser_gdf = leuser_gdf.assign(agbd_pi_lower_2 = (leuser_gdf['agbd_t'] - tse)**2 * \
                                    leuser_gdf['bias_correction_value'])
leuser_gdf = leuser_gdf.assign(agbd_pi_upper_2 = (leuser_gdf['agbd_t'] + tse)**2 * \
                                    leuser_gdf['bias_correction_value'])
# plotting agbd
ax = leuser_gdf.plot.scatter(x ='distance', y='agbd', s=15, ylabel=ylabel, xlabel=xlabel,
                        figsize=(20, 8), grid=True, color='black', 
                             label="agbd (aboveground biomass density)")
# figure title
fig_n += 1
ax.set_title(f'''
Figure {fig_n}. {ylabel} prediction interval at two confidence levels (90% and 99%) \
near Mt. Leuser, Indonesia for {beam0110.name} of {GEDIL4A} \
(n= {str(len(leuser_gdf.index))}, {len(leuser_gdf[leuser_gdf['agbd'].isnull()].index)} \
with agbd fill values)
''')

# getting alpha attribute from the agbd_prediction group
alpha =  beam0110['agbd_prediction'].attrs['alpha'] 
# plotting agbd_pi_upper/lower as fill area

ax.fill_between(leuser_gdf['distance'], leuser_gdf['agbd_pi_lower_2'],
                leuser_gdf['agbd_pi_upper_2'], alpha=0.1, color='blue',
                label=f"agbd_pi_lower/agbd_pi_upper (prediction interval, alpha={alpha_2})")
ax.fill_between(leuser_gdf['distance'], leuser_gdf['agbd_pi_lower'],
                leuser_gdf['agbd_pi_upper'], alpha=0.2, color='green',
                label=f"agbd_pi_lower/agbd_pi_upper (prediction interval, alpha={alpha})")
ax.legend()
plt.show()

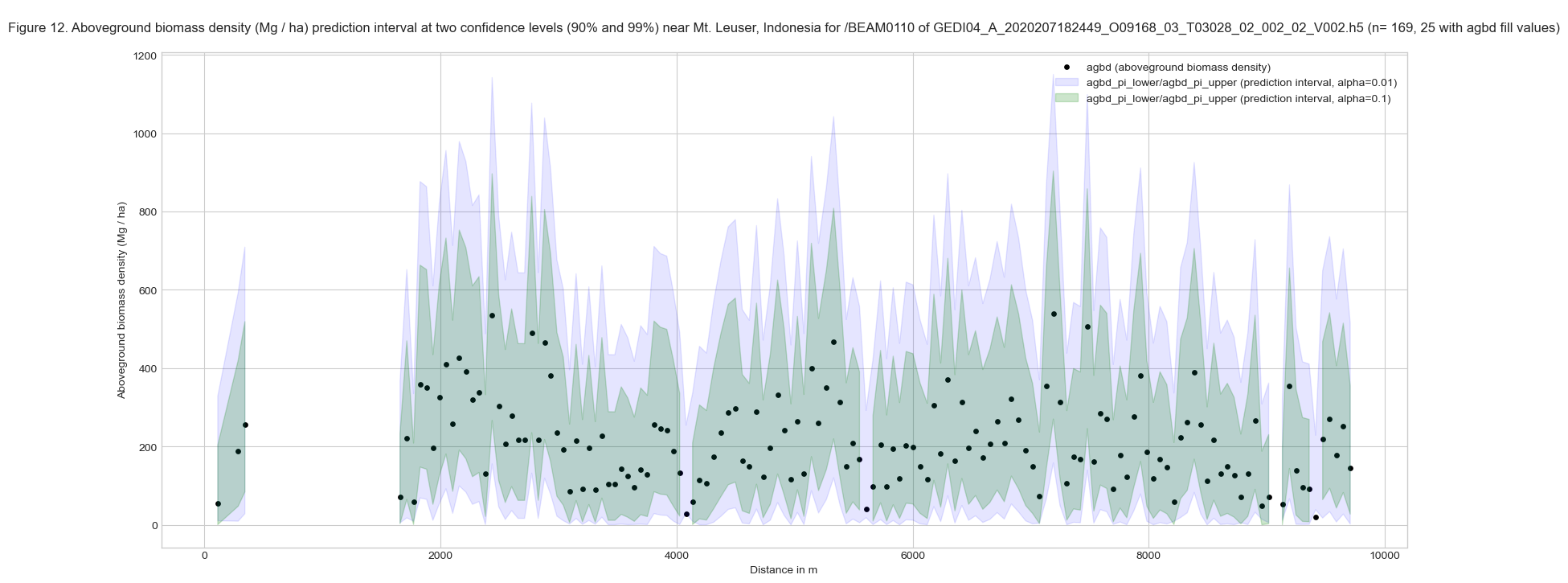
As noted above in Section 7, the subgroup agbd_prediction provides AGBD estimates for all seven algorithm settings groups (a1-6 and a10). Let’s plot all of them together. For clarity, we will plot selected shots in the following figure.

## x, y labels
ylabel = f"{beam0110['agbd'].attrs['long_name']} ({beam0110['agbd'].attrs['units']})"
xlabel = 'Distance in m'

# plotting agbd
ax = leuser_gdf[-55:-15].plot.scatter(x ='distance', y='agbd', s=100, ylabel=ylabel,
                                      xlabel=xlabel, figsize=(20, 7), grid=True,
                                      marker = "$\u25EF$", alpha=0.5, color='black',
                                      label="agbd")
l2a_alg_count =  beam0110['agbd_prediction'].attrs['l2a_alg_count']

for i in range(l2a_alg_count):
    if i == 6:
        i = 10
    else:
        i += 1
    agbd_aN = 'agbd_a' +  str(i)
    # plotting agbd
    leuser_gdf[-55:-15].plot.line(ax=ax, x ='distance', y=agbd_aN, ylabel=ylabel,
                                  xlabel=xlabel, figsize=(20, 8), grid=True,
                                  color=cmap(i), style='--o', alpha=0.6, label=agbd_aN)
for i, row in leuser_gdf[-55:-15].iterrows():
    ax.annotate(row["selected_algorithm"], (row["distance"],row["agbd"]+15))

# figure title
fig_n += 1
ax.set_title(f'''
Figure {fig_n}. {ylabel} near Mt. Leuser, Indonesia for {beam0110.name} of {GEDIL4A}.
The selected algorithm setting group for each shot is labeled and highlighted with \
a black circle.
''')
ax.legend()
plt.show()

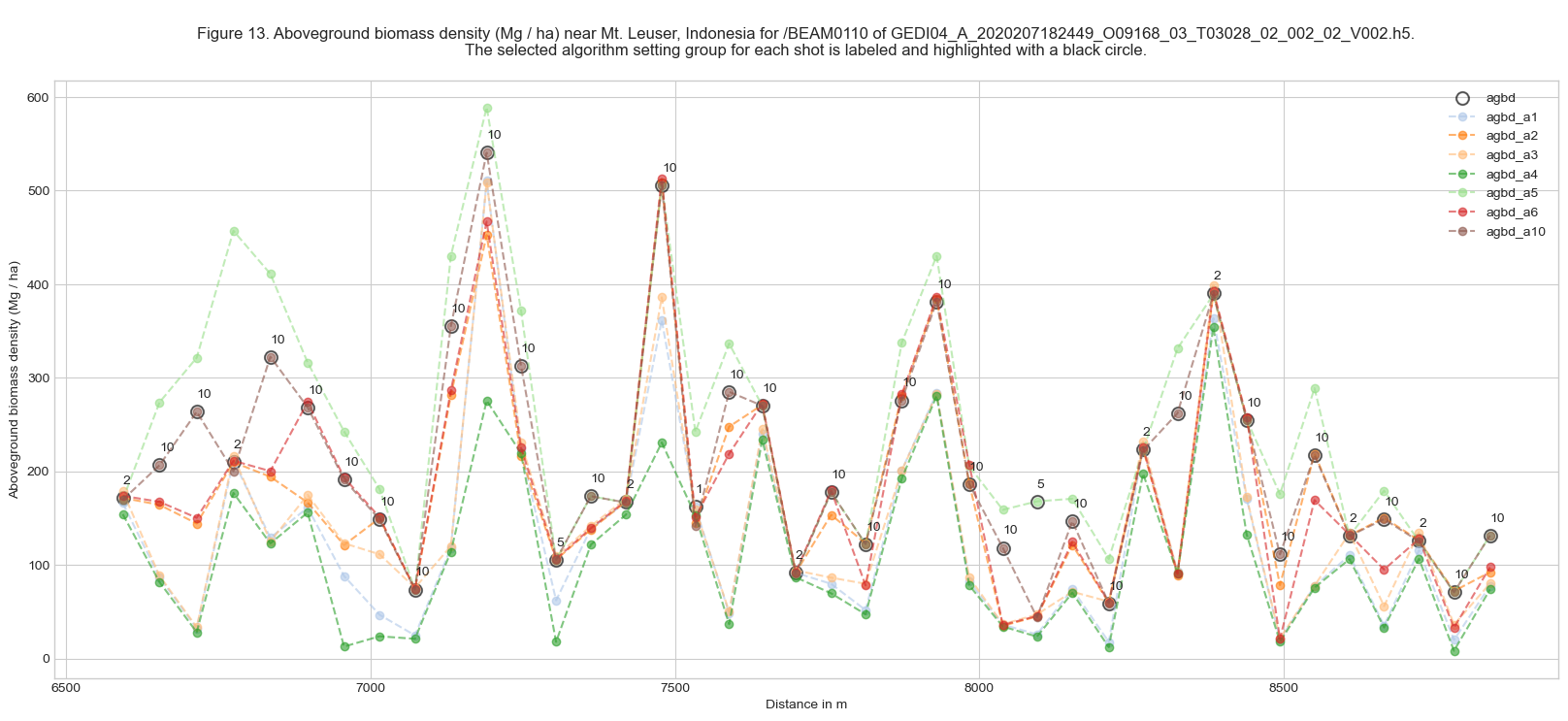
Figure 13 above shows the variability of the predicted biomass among the different algorithm setting groups.

9. Predictor variables

The xvar variable provides predictor variables. Let’s print the number of shots per predict_stratum in the leuser_gdf subset.

leuser_gdf.predict_stratum.value_counts()

predict_stratum
EBT_SAs    169
Name: count, dtype: int64

As shown above, all the GEDI shots near Mt. Leuser is classified as EBT_SAs prediction stratum (evergreen broadleaf trees PFT and South Asia region). The AGBD prediction model for EBT_SAs is given in Table 3 above as: AGBD = -104.9654541015625 + 6.802174091339111 x RH_50 + 3.9553122520446777 x RH_98.

The xvar variable has 4 columns, which we read into the dataframe above as xvar_1, xvar_2, xvar_3, and xvar_4. Let’s print the columns.

tbl_n += 1
caption = f'Table {tbl_n}. Predictor variables for the shots near Mt. Leuser, Indonesia \
for {beam0110.name} of {GEDIL4A}'
leuser_gdf[['xvar_1', 'xvar_2', 'xvar_3', 'xvar_4']].head().style.set_caption(caption)

Table 9. Predictor variables for the shots near Mt. Leuser, Indonesia for /BEAM0110 of GEDI04_A_2020207182449_O09168_03_T03028_02_002_02_V002.h5

	xvar_1	xvar_2	xvar_3	xvar_4
shot_number
91680600300633705	nan	nan	nan	nan
91680600300633706	nan	nan	nan	nan
91680600300633707	10.310674	10.592922	0.000000	0.000000
91680600300633708	10.689247	11.437220	0.000000	0.000000
91680600300633709	10.914211	11.594396	0.000000	0.000000

Since the linear model for EBT_SAs prediction stratum has only two predictor variables, RH_50 and RH_98, the columns xvar_3 and xvar_4 in the above table are filled with zero values.

The xvar predictors are transformed and as well as offset applied. Table 3 above shows that square-root (sqrt) transformation is applied to the EBT_SAs prediction stratum both x- and y- variables, and a predictor offset (predictor_offset) of 100 are applied. We will need the offset and transformation to derive the true RH metric, and plot them along with agbd value.

# deriving true RH metric
leuser_gdf['xvar_1_true']=leuser_gdf['xvar_1']**2-100
leuser_gdf['xvar_2_true']=leuser_gdf['xvar_2']**2-100

# plotting xvar_1_true (smaller green dots)
ax = leuser_gdf.plot.line(x ='distance', y='xvar_1_true', figsize=(20, 8), grid=True,
                          color='green', style='o', alpha=0.4, markersize=7,
                          label='Corrected xvar_1 (RH50)')

# adding xvar_2_true as stem plot (larger green dots)
markerline, stemline, baseline = ax.stem(leuser_gdf['distance'], leuser_gdf['xvar_2_true'],
                                         linefmt='-g', markerfmt='C2o', basefmt='C2-',
                                         label='Corrected xvar_2 (RH98)')
plt.setp(stemline, linewidth = 1.0, alpha=0.6)
plt.setp(markerline, markersize = 15, alpha=0.6)
plt.setp(baseline, linewidth = 0)

# adding agbd in the secondary axis
ax2 = ax.twinx()
markerline, stemline, baseline = ax2.stem(leuser_gdf['distance'], leuser_gdf['agbd'],
                                          linefmt='-r', markerfmt='C5o', basefmt='C2-',
                                        label='agbd (mg/ha)')
plt.setp(markerline, markersize = 0)
plt.setp(stemline, linewidth = 3.0, alpha=0.2)
plt.setp(baseline, linewidth = 0)
# figure title
fig_n += 1
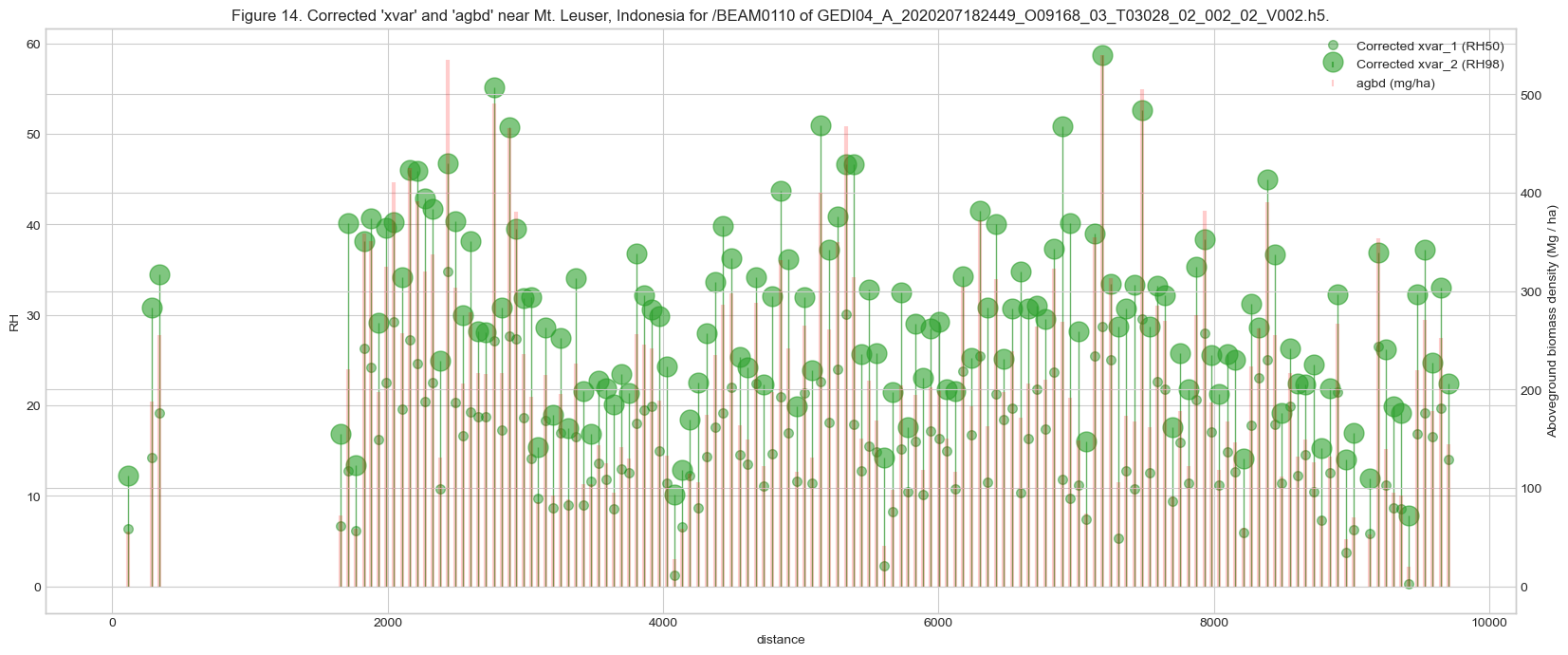
ax.set_title(f'''Figure {fig_n}. Corrected 'xvar' and 'agbd' near Mt. Leuser, Indonesia \
for {beam0110.name} of {GEDIL4A}.''')
# ylabels
ax.set_ylabel('RH')
ax2.set_ylabel(ylabel)
# legend
lines, labels = ax.get_legend_handles_labels()
lines2, labels2 = ax2.get_legend_handles_labels()
ax.legend(lines + lines2, labels + labels2, loc=0)
plt.show()

10. Flag variables

Different flag variables are included for each shot. Most of these flags originate from lower-level products such as GEDI L2A, while some of the flags are specific to the GEDI L4A dataset. Let’s print all the flag variables’ names and descriptions.

data = []
# loop over all the variables within BEAM0110 group
for v in beam0110.keys():
    var = beam0110[v]
    source = ''
    # if the key is a subgroup assign GROUP tag
    if isinstance(var, h5py.Group):
        for v2 in var.keys():
            var2 = var[v2]
            if v2.endswith('flag'):
                if 'source' in var2.attrs.keys():
                    source = var2.attrs['source']
                data.append([v2, var2.attrs['description'], source, var.name])
                
    else:
        if v.endswith('flag'):
            if 'source' in var.attrs.keys():
                source = var.attrs['source']
            data.append([v, var.attrs['description'], source, beam0110.name])

# print all variable name and attributes as a table

headers = ["variable", "description", "source", "group"]
df = pd.DataFrame(data, columns=headers)
tbl_n += 1
caption = f'Table {tbl_n}. Flag variables for GEDI L4A {beam_str} group'
df.style.set_caption(caption).hide(axis="index")

Table 10. Flag variables for GEDI L4A BEAM0110 group

variable	description	source	group
algorithm_run_flag	The L4A algorithm is run if this flag is set to 1. This flag selects data which have sufficient waveform fidelity for AGBD estimation.		/BEAM0110
degrade_flag	Flag indicating degraded state of pointing and/or positioning information	L2A	/BEAM0110
stale_return_flag	Flag from digitizer indicating the real-time pulse detection algorithm did not detect a return signal above its detection threshold within the entire 10 km search window. The pulse location of the previous shot was used to select the telemetered waveform.	L2A	/BEAM0110/geolocation
l2_quality_flag	Flag identifying the most useful L2 data for biomass predictions		/BEAM0110
l4_quality_flag	Flag simplifying selection of most useful biomass predictions		/BEAM0110
leaf_off_flag	GEDI 1 km EASE 2.0 grid flag derived from leaf_off_doy, leaf_on_doy and pft_class, indicating if the observation was recorded during leaf-off conditions in deciduous needleleaf or broadleaf forests and woodlands. 1 = leaf-off and 0 = leaf-on.		/BEAM0110/land_cover_data
predictor_limit_flag	Predictor value is outside the bounds of the training data (0=In bounds; 1=Lower bound; 2=Upper bound)		/BEAM0110
response_limit_flag	Prediction value is outside the bounds of the training data (0=In bounds; 1=Lower bound; 2=Upper bound)		/BEAM0110
selected_mode_flag	Flag indicating status of selected_mode	L2A	/BEAM0110
surface_flag	Indicates elev_lowestmode is within 300m of Digital Elevation Model (DEM) or Mean Sea Surface (MSS) elevation	L2A	/BEAM0110

Let’s plot algorithm_run_flag, l2_quality_flag, and l4_quality_flag into a plot.

# plot flags as stacked bar diagram
ax = leuser_gdf.plot(y=['algorithm_run_flag', 'l2_quality_flag','l4_quality_flag'],
                     alpha=0.4, kind='bar', figsize=(22, 8), stacked=True,
                     use_index=True,legend=True)
# plot agbd in the secondary y-axis as line
ax2 = ax.twinx()
ax2.plot(leuser_gdf[['agbd']].values, linestyle='-', alpha=0.6, marker='o',
         linewidth=2.0, color ='black')
# figure title
fig_n += 1
ax.set_title(f'''
Figure {fig_n}. Flag variables and {ylabel} near Mt. Leuser, Indonesia for \
{beam0110.name} of {GEDIL4A}. 
A flag value of 1 in the figure indicates good values. \
(n= {str(len(leuser_gdf.index))}, {len(leuser_gdf[leuser_gdf['agbd'].isnull()].index)} \
with agbd fill values)
''')
# labels
ax.set_ylabel("flags")
ax2.set_ylabel(ylabel)
plt.show()

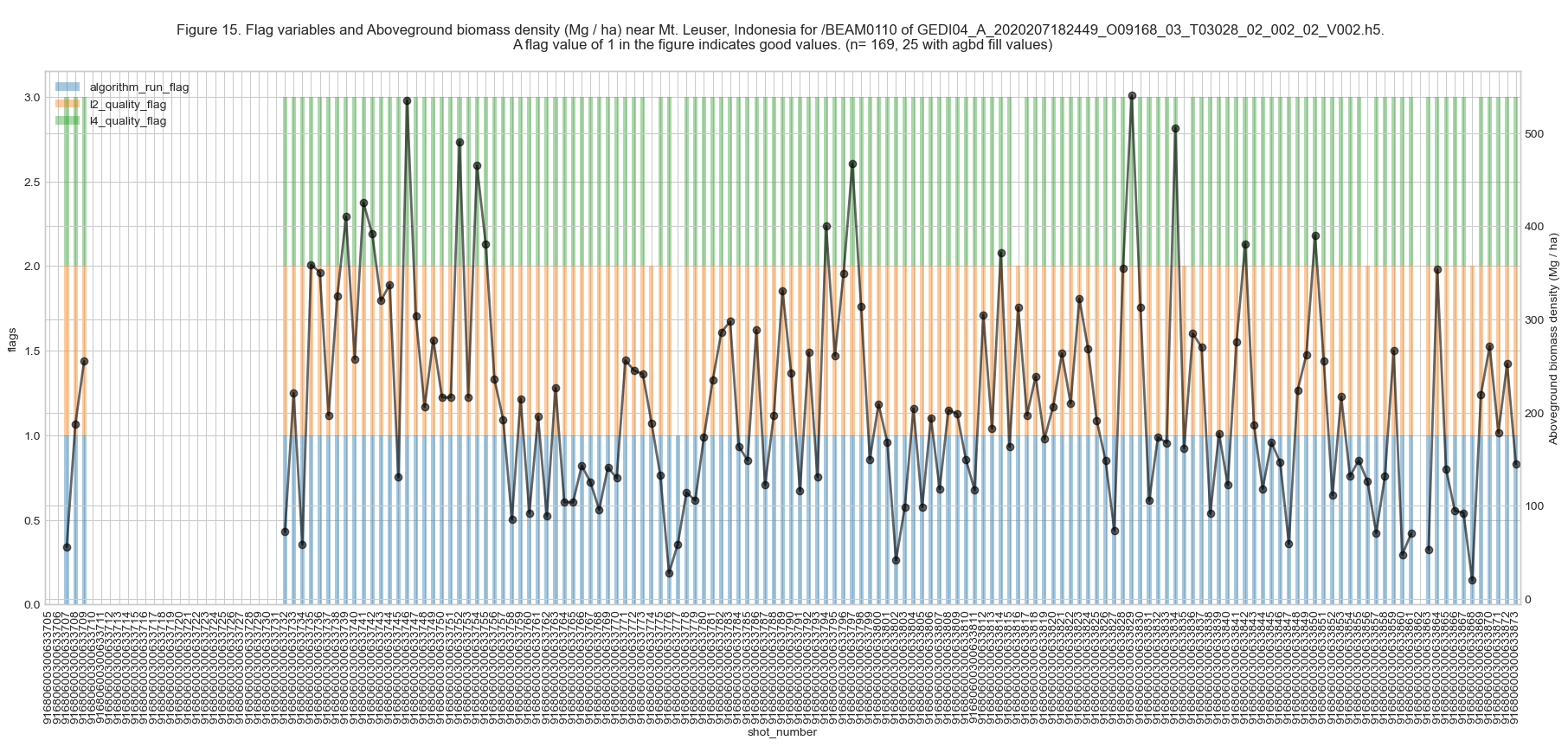
The algorithm_run_flag set is set to 1 when the shot quality is good to run the GEDIL4_A algorithm. When the algorithm is not run for the shot (indicated by algorithm_run_flag=0), all the AGBD variables will be set to the fill values (-9999). The l2_quality_flag identifies shots with good GEDI L2A quality metrics for the prediction of AGBD. The l4_quality_flag identifies shots that are representative of the applied AGBD models. Let’s apply both l2_quality_flag and l4_quality_flag to the dataframe.

qidx = (leuser_gdf['l2_quality_flag'] == 1) & (leuser_gdf['l4_quality_flag'] == 1)
leuser_gdf = leuser_gdf[qidx]

# close the GEDI L4A HDF file
hf.close()

Now, the dataframe leuser_gdf contains all the rows where both l2_quality_flag and l4_quality_flag filters are applied. Refer to the GEDI L4A ATBD and GEDI L4A Common Queries documents for more details about the quality flags.

11. Final Note

As we saw in this tutorial, in addition to AGBD estimates, a GEDI L4A file has information about predictor variables from the lower level GEDI products and other associated variables derived from multiple sensors such as MODIS, VIIRS, TanDEM-X, and Landsat, among others. GEDI generates ~15-16 orbits each day. GEDI is still collecting data every day and will do so for the next few years, which is an immense amount of data at our hands.

References

[1]

R.O. Dubayah, J. Armston, J.R. Kellner, L. Duncanson, S.P. Healey, P.L. Patterson, S. Hancock, H. Tang, J. Bruening, M.A. Hofton, J.B. Blair, and S.B. Luthcke. GEDI L4A Footprint Level Aboveground Biomass Density, Version 2.1. 2022. doi:10.3334/ORNLDAAC/2056.

[2]

J.R. Kellner, J. Armston, and L. Duncanson. Algorithm theoretical basis document for GEDI footprint aboveground biomass density. Earth and Space Science, 9:e2022EA002516, 2022. doi:10.1029/2022EA002516.